题目内容
17．某几何体的三视图如图所示，则该几何体的表面积为（ ）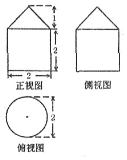
| A． | $\frac{7π}{3}$ | B． | $8+\frac{π}{3}$ | C． | $（{4+\sqrt{2}}）π$ | D． | $（{5+\sqrt{2}}）π$ |
分析 由三视图知几何体是圆锥与圆柱的组合体，结合图中数据计算它的表面积即可．
解答 解：由三视图知几何体是圆锥与圆柱的组合体，
且圆锥、圆柱的底面圆半径为1，圆柱的高为2，圆锥的高为1，
所以该组合体的表面积为
S=S圆柱+S圆锥侧=π•12+2π•1•2+π•1•$\sqrt{{1}^{2}{+1}^{2}}$=（5+$\sqrt{2}$）π．
故选：D．
点评 本题考查了空间几何体三视图的应用以及圆锥、圆柱表面积的计算问题，是基础题．
练习册系列答案
优加精卷系列答案
相关题目
8．已知5件产品中有2件次品，现逐一检测，直至能确定所有次品为止，记检测的次数为ξ，则Eξ=（ ）
| A． | 3 | B． | $\frac{7}{2}$ | C． | $\frac{18}{5}$ | D． | 4 |
5．$\frac{sin10°}{1-\sqrt{3}tan10°}$=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 1 |
12．运行如图所示的程序，若输入x的值为256，则输出的y值是（ ）
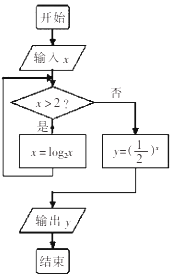
| A． | $\frac{1}{3}$ | B． | -3 | C． | 3 | D． | $-\frac{1}{3}$ |