题目内容
若直线斜率k满足-
≤k≤
，则直线倾斜角的取值范围是 ．
| 3 |
| 3 |
考点：直线的斜率
专题：直线与圆
分析：设直线的倾斜角为α，由直线斜率k满足-
≤k≤
，得-
≤tanα＜0，或0≤tanα≤
，由此能求出直线倾斜角的取值范围．
| 3 |
| 3 |
| 3 |
| 3 |
解答：
解：设直线的倾斜角为α，
∵直线斜率k满足-
≤k≤
，
∴-
≤tanα＜0，或0≤tanα≤
，
∴
≤α＜π或0≤α≤
．
∴直线倾斜角的取值范围是[
，π）∪[0，
]．
故答案为：[
，π）∪[0，
]．
∵直线斜率k满足-
| 3 |
| 3 |
∴-
| 3 |
| 3 |
∴
| 2π |
| 3 |
| π |
| 3 |
∴直线倾斜角的取值范围是[
| 2π |
| 3 |
| π |
| 3 |
故答案为：[
| 2π |
| 3 |
| π |
| 3 |
点评：本题考查直线的倾斜角的取值范围的求法，是基础题，解题时要认真审题．
练习册系列答案
相关题目
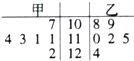某质检机构检测某产品的质量是否合格，在甲乙两厂的匀速运行的自动包装传送带上每隔10分钟抽一包产品，称其质量（单位：克），分别记录抽查数据，获得质量数据茎叶图（如图）．已知集合M={x|x-2＞0，x∈R}，N={y|y=
，x∈R}，则M∪N等于（ ）
| x2+1 |
| A、{x|x≥1} |
| B、{x|1≤x＜2} |
| C、{x|x＞2} |
| D、{x|x＞2或x＜0} |