题目内容
已知函数f(x)是R上的奇函数,当x>0时,f(x)=x2-4x+3.
(1)求函数f(x)的解析式;
(2)作出函数f(x)的图象,并根据图象讨论直线y=k(k∈R)与函数y=f(x)的图象的交点个数.
(1)求函数f(x)的解析式;
(2)作出函数f(x)的图象,并根据图象讨论直线y=k(k∈R)与函数y=f(x)的图象的交点个数.
考点:函数奇偶性的性质,二次函数的性质
专题:
分析:(1)利用奇函数定义求解转化,
(2)作出图象,根据图象讨论的答案.
(2)作出图象,根据图象讨论的答案.
解答:
解:(1)∵函数f(x)是R上的奇函数,
∴f(-x)=-f(x)
即f(0)=0
∵当x>0时,f(x)=x2-4x+3,
∴设x<0时,则-x>0,f(x)=-f(-x)=-[(-x)2-4(-x)+3]
即f(x)═-x2-4x-3,x<0
f(x)=
(2)特别强调的是图中y 轴上的点(0,3),(0-3)为虚点,图中画不出虚点符号,
f(2)=-1,f(-2)=1
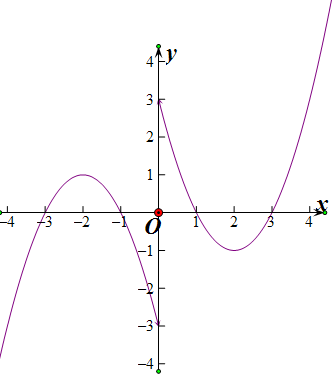
由图可判断直线y=k(k∈R)与函数y=f(x)的图象的交点个数:
(1)k≥3或k≤-3时,有1个交点;
(2)-3<k<-1或1<k<3时,有2个交点; (3)k=±1时,有3个交点;
(4)-1<k<0或0<k<1时,有4个交点; (5)k=0时,有5个交点.
∴f(-x)=-f(x)
即f(0)=0
∵当x>0时,f(x)=x2-4x+3,
∴设x<0时,则-x>0,f(x)=-f(-x)=-[(-x)2-4(-x)+3]
即f(x)═-x2-4x-3,x<0
f(x)=
|
(2)特别强调的是图中y 轴上的点(0,3),(0-3)为虚点,图中画不出虚点符号,
f(2)=-1,f(-2)=1
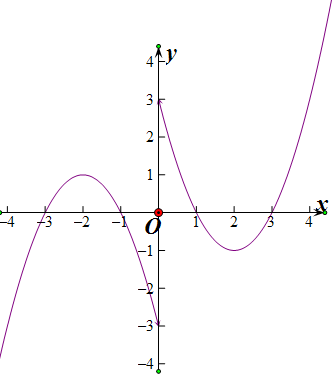
由图可判断直线y=k(k∈R)与函数y=f(x)的图象的交点个数:
(1)k≥3或k≤-3时,有1个交点;
(2)-3<k<-1或1<k<3时,有2个交点; (3)k=±1时,有3个交点;
(4)-1<k<0或0<k<1时,有4个交点; (5)k=0时,有5个交点.
点评:本题综合考查了函数的图象性质,要求的能力较高.

练习册系列答案
相关题目

