题目内容
5.若实数x,y满足约束条件$\left\{\begin{array}{l}{x-y-2≤0}\\{x+2y-7≥0}\\{y-3≤0}\end{array}\right.$,则z=$\frac{y}{x+1}$的最大值为( )| A. | $\frac{3}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{5}{14}$ |
分析 作出不等式组对应的平面区域,利用直线的斜率的几何意义进行求解即可.
解答 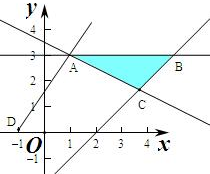 解:作出不等式组对应的平面区域如图,z=$\frac{y}{x+1}$的几何意义是区域内的点到点D(-1,0)的斜率,
解:作出不等式组对应的平面区域如图,z=$\frac{y}{x+1}$的几何意义是区域内的点到点D(-1,0)的斜率,
由图象知AD的斜率最大,
由$\left\{\begin{array}{l}{y-3=0}\\{x+2y-7=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$,即A(1,3),
此时z=$\frac{3}{1+1}$=$\frac{3}{2}$,
故选:A.
点评 本题主要考查线性规划的应用,利用直线的斜率公式,结合数形结合是解决本题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
20.若集合A={-2,-1,0,1,2},B={x|2x>1},则A∩B=( )
| A. | {-1,2} | B. | {0,1} | C. | {1,2} | D. | {0,1,2} |
14.某学校采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做视力检查,现将800名学生从1到800进行编号.已知从1-16这16个数中被抽到的数是11,则编号在33-48中被抽到的数是( )
| A. | 39 | B. | 41 | C. | 43 | D. | 45 |
15.已知数列{an}中,a1=1,若an+1=3an+2(n∈N*),则数列{an}的通项公式an=( )
| A. | 2×3n-1 | B. | 2×3n-1-1 | C. | 2×3n-1+1 | D. | 3×2n-1-2 |
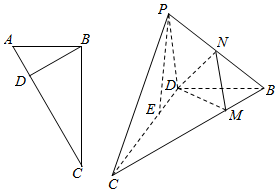 如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.
如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.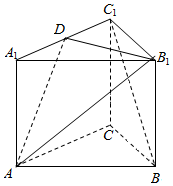 已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.
已知三棱柱ABC-A1B1C1,△ABC是正三角形,直线AA1⊥平面A1B1C1,D是棱A1C1的中点.