题目内容
设x、y满足约束条件
,则使z=x+2y取得最大值时的最优解是( )
|
| A、(0,2) |
| B、(2,0) |
| C、(0,1) |
| D、(1,0) |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:
由z=x+2y得y=-
x+
,
平移直线y=-
x+
,由图象可知当直线y=-
x+
经过点A时,
直线y=-
x+
的截距最大,此时z最大,
由
,解得
,
即A(0,2),
则z=x+2y取得最大值时的最优解是(0,2),
故选:A.

由z=x+2y得y=-
| 1 |
| 2 |
| z |
| 2 |
平移直线y=-
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
直线y=-
| 1 |
| 2 |
| z |
| 2 |
由
|
|
即A(0,2),
则z=x+2y取得最大值时的最优解是(0,2),
故选:A.
点评:本题主要考查线性规划的应用,利用z的几何意义,通过数形结合是解决本题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
下列四个命题中,正确的是( )
| A、“若xy=0,则x=0且y=0”的逆否命题 |
| B、“若ac2>bc2则a>b”的逆命题 |
| C、若“m>2,则不等式x2-2x+m>0的解集为R” |
| D、“正方形是菱形”的否命题 |
下列命题为真命题的是( )
①如果命题“?p”与命题“p∨q”都是真命题,那么命题q一定是真命题;
②“若x2+y2=0,则x,y全为0”的否命题;
③“若x∈A∩B,则x∈A∪B”的逆命题;
④若?p是q的必要条件,则p是?q的充分条件;
⑤到两定点F1(-2,0),F2(2,0)距离之和为定值2的动点轨迹是椭圆.
①如果命题“?p”与命题“p∨q”都是真命题,那么命题q一定是真命题;
②“若x2+y2=0,则x,y全为0”的否命题;
③“若x∈A∩B,则x∈A∪B”的逆命题;
④若?p是q的必要条件,则p是?q的充分条件;
⑤到两定点F1(-2,0),F2(2,0)距离之和为定值2的动点轨迹是椭圆.
| A、①②⑤ | B、①③④ |
| C、②③ | D、①②④ |
执行如图所不的程序框图,则输出的x的值是( )


| A、3 | B、4 | C、6 | D、8 |
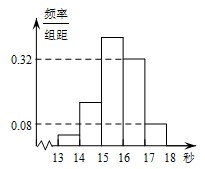 已知某年级1000名学生的百米跑成绩全部介于13秒与18秒之间,为了了解学生的百米跑成绩情况,随机抽取了若干学生的百米跑成绩,并按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为1:4:10,且第二组的频数为8.
已知某年级1000名学生的百米跑成绩全部介于13秒与18秒之间,为了了解学生的百米跑成绩情况,随机抽取了若干学生的百米跑成绩,并按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为1:4:10,且第二组的频数为8.