题目内容
如图1,直角梯形ABCD中,∠ABC=90°,AB=BC=2AD=4,点E、F分别是AB、CD的中点,点G在EF上,沿EF将梯形AEFD翻折,使平面AEFD⊥平面EBCF,如图2.
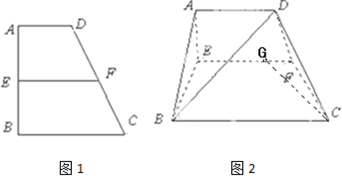
(Ⅰ)当AG+GC最小时,求证:BD⊥CG;
(Ⅱ)当2VB-ADGE=VD-GBCF时,求二面角D-BG-C平面角的余弦值.

(Ⅰ)当AG+GC最小时,求证:BD⊥CG;
(Ⅱ)当2VB-ADGE=VD-GBCF时,求二面角D-BG-C平面角的余弦值.
考点:与二面角有关的立体几何综合题,平面与平面垂直的性质
专题:空间角
分析:(Ⅰ)由已知条件推导出AE⊥EF,AE⊥BE,BE⊥EF,建立空间坐标系E-xyz,利用向量法能求出BD⊥CG.
(Ⅱ)法一:设EG=k,由AD∥平面EFCB,得到点D到平面EFCB的距离为即为点A到平面EFCB的距离.分别求出平面DBG的法向量和面BCG的一个法向量,利用向量法能求出二面角平面角的余弦值.
(Ⅱ)法二:由已知条件指法训练出EG=1,过点D作DH⊥EF,垂足H,过点H作BG延长线的垂线垂足O,连接OD.由已知条件推导出∠DOH就是所求的二面角D-BG-C的平面角,由此能求出此二面角平面角的余弦值.
(Ⅱ)法一:设EG=k,由AD∥平面EFCB,得到点D到平面EFCB的距离为即为点A到平面EFCB的距离.分别求出平面DBG的法向量和面BCG的一个法向量,利用向量法能求出二面角平面角的余弦值.
(Ⅱ)法二:由已知条件指法训练出EG=1,过点D作DH⊥EF,垂足H,过点H作BG延长线的垂线垂足O,连接OD.由已知条件推导出∠DOH就是所求的二面角D-BG-C的平面角,由此能求出此二面角平面角的余弦值.
解答:
(Ⅰ)证明:∵点E、F分别是AB、CD的中点,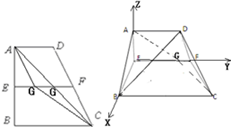
∴EF∥BC,又∠ABC=90°,∴AE⊥EF,
∵平面AEFD⊥平面EBCF,
∴AE⊥平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,
如图建立空间坐标系E-xyz.…(2分)
翻折前,连结AC交EF于点G,此时点G使得AG+GC最小.
EG=
BC=2,又∵EA=EB=2.
则A(0,0,2),B(2,0,0),C(2,4,0),
D(0,2,2),E(0,0,0),G(0,2,0),
∴
=(-2,2,2),
=(-2,-2,0)
∴
•
=(-2,2,2)(-2,-2,0)=0,
∴BD⊥CG.…(5分)
(Ⅱ)解法一:设EG=k,∵AD∥平面EFCB,
∴点D到平面EFCB的距离为即为点A到平面EFCB的距离.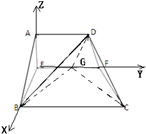
∵S四形GBCF=
[(3-k)+4]×2=7-k,
∴VD-GBCF=
•S四形GBCF•AE=
(7-k),
又VB-ADGE=
S四形ADGE•BE=
(2+k),
∵2VB-ADGE=VD-GBCF,∴
(2+k)=
(7-k),
∴k=1即EG=1…(8分)
设平面DBG的法向量为
=(x,y,z),∵G(0,1,0),
∴
=(-2,1,0),
=(-2,2,2),
则
,即
取x=1,则y=2,z=-1,∴
=(1,2,-1)…(10分)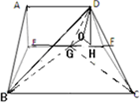
面BCG的一个法向量为
=(0,0,1)
则cos<
,
>=
=-
…(12分)
由于所求二面角D-BF-C的平面角为锐角,
所以此二面角平面角的余弦值为
…(13分)
(Ⅱ)解法二:由解法一得EG=1,过点D作DH⊥EF,垂足H,
过点H作BG延长线的垂线垂足O,连接OD.
∵平面AEFD⊥平面EBCF,
∴DH⊥平面EBCF,∴OD⊥OB,
∴∠DOH就是所求的二面角D-BG-C的平面角.…(9分)
由于HG=1,在△OHG中OH=
,
又DH=2,在△DOH中tan∠DOH=
=
…(11分)
∴此二面角平面角的余弦值为
.…(13分)

∴EF∥BC,又∠ABC=90°,∴AE⊥EF,
∵平面AEFD⊥平面EBCF,
∴AE⊥平面EBCF,AE⊥EF,AE⊥BE,又BE⊥EF,
如图建立空间坐标系E-xyz.…(2分)
翻折前,连结AC交EF于点G,此时点G使得AG+GC最小.
EG=
| 1 |
| 2 |
则A(0,0,2),B(2,0,0),C(2,4,0),
D(0,2,2),E(0,0,0),G(0,2,0),
∴
| BD |
| CG |
∴
| BD |
| CG |
∴BD⊥CG.…(5分)
(Ⅱ)解法一:设EG=k,∵AD∥平面EFCB,
∴点D到平面EFCB的距离为即为点A到平面EFCB的距离.

∵S四形GBCF=
| 1 |
| 2 |
∴VD-GBCF=
| 1 |
| 3 |
| 2 |
| 3 |
又VB-ADGE=
| 1 |
| 3 |
| 2 |
| 3 |
∵2VB-ADGE=VD-GBCF,∴
| 4 |
| 3 |
| 2 |
| 3 |
∴k=1即EG=1…(8分)
设平面DBG的法向量为
| n1 |
∴
| BG |
| BD |
则
|
|
取x=1,则y=2,z=-1,∴
| n |

面BCG的一个法向量为
| n2 |
则cos<
| n1 |
| n2 |
| ||||
|
| ||
| 6 |
由于所求二面角D-BF-C的平面角为锐角,
所以此二面角平面角的余弦值为
| ||
| 6 |
(Ⅱ)解法二:由解法一得EG=1,过点D作DH⊥EF,垂足H,
过点H作BG延长线的垂线垂足O,连接OD.
∵平面AEFD⊥平面EBCF,
∴DH⊥平面EBCF,∴OD⊥OB,
∴∠DOH就是所求的二面角D-BG-C的平面角.…(9分)
由于HG=1,在△OHG中OH=
2
| ||
| 5 |
又DH=2,在△DOH中tan∠DOH=
| DH |
| OH |
| 5 |
∴此二面角平面角的余弦值为
| ||
| 6 |
点评:本题考查异面直线垂直的证明,考查二面角的平面角的余弦值的求法,解题时要注意向量法的合理运用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
设x、y满足约束条件
,则使z=x+2y取得最大值时的最优解是( )
|
| A、(0,2) |
| B、(2,0) |
| C、(0,1) |
| D、(1,0) |
 “开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.
“开门大吉”是某电视台推出的游戏益智节目.选手面对1-4号4扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:20~30;30~40(单位:岁),其猜对歌曲名称与否人数如图所示.  如图,设F(-c,0)是椭圆
如图,设F(-c,0)是椭圆