题目内容
求函数f(x)=
的值域.
| ||
| x-5 |
考点:函数的值域
专题:函数的性质及应用
分析:利用换元法,设
=t,表示x,求出f(t)的值域即得f(x)的值域.
| x+4 |
解答:
解:设
=t,(其中t≥0);
∴x=t2-4;
∴y=f(t)=
=
=
;
∵t≥0,∴t+3≥3,
∴0<
≤
,
又t≠3,
∴y≠
;
∴f(x)的值域是(0,
)∪(
,
].
| x+4 |
∴x=t2-4;
∴y=f(t)=
| t-3 |
| (t2-4)-5 |
=
| t-3 |
| (t-3)(t+3) |
=
|
∵t≥0,∴t+3≥3,
∴0<
| 1 |
| t+3 |
| 1 |
| 3 |
又t≠3,
∴y≠
| 1 |
| 6 |
∴f(x)的值域是(0,
| 1 |
| 6 |
| 1 |
| 6 |
| 1 |
| 3 |
点评:本题考查了求函数值域的问题,解题的关键是设
=t,利用换元法,求出函数的值域.
| x+4 |

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
等差数列x1,x2,x3…x9的公差为1,随机变量ξ等可能的取值x1,x2,x3…x9,则方差D(ξ)为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设x、y满足约束条件
,则使z=x+2y取得最大值时的最优解是( )
|
| A、(0,2) |
| B、(2,0) |
| C、(0,1) |
| D、(1,0) |
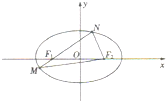 如图,椭圆E:
如图,椭圆E: