Question

12．在平行四边形中，AB=4，AD=3，∠BAD=60°，点E在BC上，且$\overrightarrow{BE}$=2$\overrightarrow{EC}$，F是DC的中点，则$\overrightarrow{AE}$•$\overrightarrow{BF}$=2．

Answer 1

分析 建立平面直角坐标系，求出$\overrightarrow{AE}，\overrightarrow{BF}$的坐标进行计算即可．

解答 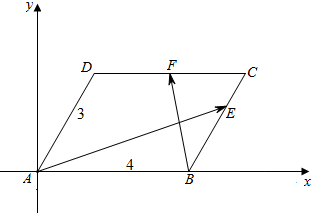以AB为x轴，以A为原点建立平面直角坐标系，如图，
则A（0，0），B（4，0），C（$\frac{11}{2}$，$\frac{3\sqrt{3}}{2}$），D（$\frac{3}{2}$，$\frac{3\sqrt{3}}{2}$），E（5，$\sqrt{3}$），F（$\frac{7}{2}$，$\frac{3\sqrt{3}}{2}$）．
∴$\overrightarrow{AE}$=（5，$\sqrt{3}$），$\overrightarrow{BF}$=（-$\frac{1}{2}$，$\frac{3\sqrt{3}}{2}$），
∴$\overrightarrow{AE}$•$\overrightarrow{BF}$=5×（-$\frac{1}{2}$）+$\sqrt{3}$×$\frac{3\sqrt{3}}{2}$=2．
故答案为：2．

点评 本题考查了平面向量的数量积运算，属于中档题．