题目内容
11.将函数f(x)=$\sqrt{3}$cos(2x+$\frac{π}{3}$)-1的图象向左平移$\frac{π}{3}$个单位长度,再向上平移1个单位长度,得到函数g(x)的图象,则函数g(x)具有性质②③④.(填入所有正确性质的序号)①最大值为$\sqrt{3}$,图象关于直线x=-$\frac{π}{3}$对称;
②图象关于y轴对称;
③最小正周期为π;
④图象关于点($\frac{π}{4}$,0)对称;
⑤在(0,$\frac{π}{3}$)上单调递减.
分析 利用函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再利用余弦函数的图象和性质,得出结论.
解答 解:将函数f(x)=$\sqrt{3}$cos(2x+$\frac{π}{3}$)-1的图象向左平移$\frac{π}{3}$个单位长度,
得到y=$\sqrt{3}$cos[2(x+$\frac{π}{3}$)+$\frac{π}{3}$]-1=$\sqrt{3}$cos(2x+π)-1=-$\sqrt{3}$cos2x-1的图象;
再向上平移1个单位长度,得到函数g(x)=-$\sqrt{3}$cos2x 的图象.
对于函数g(x):
它的最大值为$\sqrt{3}$,由于当x=-$\frac{π}{3}$时,g(x)=$\frac{\sqrt{3}}{2}$,不是最值,故g(x)的图象不关于直线x=-$\frac{π}{3}$对称,故排除①;
由于该函数为偶函数,故它的图象关于y轴对称,故②正确;
它的最小正周期为$\frac{2π}{2}$=π,故③正确;
当x=$\frac{π}{4}$时,g(x)=0,故函数的图象关于点($\frac{π}{4}$,0)对称,故④正确;
在(0,$\frac{π}{3}$)上,2x∈(0,$\frac{2π}{3}$),g(x)不是单调函数,故排除⑤,
故答案为:②③④.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,余弦函数的图象和性质,属于中档题.

练习册系列答案
相关题目
1.一个几何体的三视图如图所示,则其表面积为( )
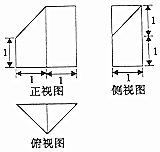

| A. | $\frac{9}{2}$+4$\sqrt{2}$ | B. | 5$+4\sqrt{2}$ | C. | 6$+4\sqrt{2}$ | D. | $\frac{13}{2}$$+4\sqrt{2}$ |
2.幂函数y=f(x)的图象经过点$(3,\root{3}{3})$,则f(x)是( )
| A. | 偶函数,且在(0,+∞)上是增函数 | |
| B. | 偶函数,且在(0,+∞)上是减函数 | |
| C. | 奇函数,且在(0,+∞)上是增函数 | |
| D. | 非奇非偶函数,且在(0,+∞)上是增函数 |
6.方程log5x-sin2x=0的根的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.设a=22.5,b=log${\;}_{\frac{1}{2}}$2.5,c=($\frac{1}{2}$)2.5,则a,b,c之间的大小关系是( )
| A. | c>b>a | B. | c>a>b | C. | a>c>b | D. | b>a>c |
3.直线2x-y-2=0绕它与y轴的交点逆时针旋转$\frac{π}{2}$所得的直线方程是( )
| A. | -x+2y-4=0 | B. | x+2y-4=0 | C. | -x+2y+4=0 | D. | x+2y+4=0 |