题目内容
12.如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{18}$的值的一个程序框图,其中判断框内应填入的条件是( )
| A. | i>9 | B. | i<9 | C. | i>18 | D. | i<18 |
分析 分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S的值,模拟循环过程可得条件.
解答 解:程序运行过程中,各变量值如下表所示:
S=0,n=2,i=1
不满足条件,第一圈:S=0+$\frac{1}{2}$,n=4,i=2,
不满足条件,第二圈:S=$\frac{1}{2}$+$\frac{1}{4}$,n=6,i=3,
不满足条件,第三圈:S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$,n=8,i=4,
…
依此类推,
不满足条件,第8圈:S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$++…+,n=18,i=9,
不满足条件,第9圈:S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$++…+$\frac{1}{18}$,n=20,i=10,
此时,应该满足条件,退出循环
其中判断框内应填入的条件是:i>9.
故选:A.
点评 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视.程序填空也是重要的考试题型,这种题考试的重点有:①分支的条件②循环的条件③变量的赋值④变量的输出.其中前两点考试的概率更大.此种题型的易忽略点是:不能准确理解流程图的含义而导致错误,属于基础题.

练习册系列答案
相关题目
2.某企业有甲乙两个分厂生产某种产品,按规定该产品的某项质量指标值落在[45,75)的为优质品,从两个分厂生产的产品中个随机抽取500件,测量这些产品的该项质量指标值,结果如表:
(1)根据以上统计数据完成下面2×2列联表,并回答是否有99%的把握认为:“两个分厂生产的产品的质量有差异”?
(2)求优质品率较高的分厂的500件产品质量指标值的样本平均数$\overline x$(同一组数据用该区间的中点值作代表)
(3)经计算,甲分厂的500件产品质量指标值的样本方差s2=142,乙分厂的500件差评质量指标值的样本方差s2=162,可认为优质品率较高的分厂的产品质量指标值X服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline x$,σ2近似为样本方差s2,由优质品率较高的厂的抽样数据,能够认为该分厂生产的产品的产品中,质量指标值不低于71.92的产品至少占全部产品的18%?
附注:
参考数据:$\sqrt{140}$≈11.92,$\sqrt{162}$≈12.73
参考公式:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
P(μ-2σ<x<μ+2σ)=0.9544,P(μ-3σ<x<μ+3σ)=0.9974.
| 分组 | [25,35) | [35,45) | [4,55) | [55,65) | [65,75) | [75,85) | [85,95) |
| 甲厂频数 | 10 | 40 | 115 | 165 | 120 | 45 | 5 |
| 乙厂频数 | 5 | 60 | 110 | 160 | 90 | 70 | 5 |
(2)求优质品率较高的分厂的500件产品质量指标值的样本平均数$\overline x$(同一组数据用该区间的中点值作代表)
(3)经计算,甲分厂的500件产品质量指标值的样本方差s2=142,乙分厂的500件差评质量指标值的样本方差s2=162,可认为优质品率较高的分厂的产品质量指标值X服从正态分布N(μ,σ2),其中μ近似为样本平均数$\overline x$,σ2近似为样本方差s2,由优质品率较高的厂的抽样数据,能够认为该分厂生产的产品的产品中,质量指标值不低于71.92的产品至少占全部产品的18%?
附注:
参考数据:$\sqrt{140}$≈11.92,$\sqrt{162}$≈12.73
参考公式:k2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
P(μ-2σ<x<μ+2σ)=0.9544,P(μ-3σ<x<μ+3σ)=0.9974.
| P(k2≥k) | 0.05 | 0.01 | 0.001 |
| h | 3.841 | 6.635 | 10.828 |
3.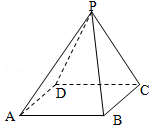 如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
 如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )
如图,在正四棱锥P-ABCD中,AB=2$\sqrt{3}$,侧面积为8$\sqrt{3}$,则它的体积为( )| A. | 4 | B. | 8 | C. | 12π | D. | 16π |
7.已知实数x,y满足ax<ay(0<a<1),则下列关系式恒成立的是( )
| A. | $\frac{1}{{{x^2}+1}}>\frac{1}{{{y^2}+1}}$ | B. | ln(x2+1)>ln(y2+1) | C. | sinx>siny | D. | x3>y3 |
2.将函数$y=sin({2x-\frac{2π}{3}})$的图象向左平移$\frac{π}{3}$个单位所得到的图象的解析式为( )
| A. | .y=sin2x | B. | .y=-sin2x | C. | .y=cos2x | D. | y=-2cosx |
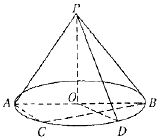 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.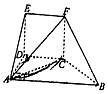 如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.
如图,几何体EF-ABCD中,DE⊥平面ABCD,CDEF是正方形,ABCD为直角梯形,AB∥CD,AD⊥DC,△ACB的腰长为$2\sqrt{2}$的等腰直角三角形.