题目内容
4.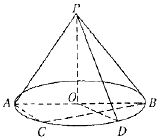 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.(Ⅰ)若弧BC的中点为D.求证:AC∥平面POD;
(Ⅱ)如果△PAB面积是9,求此圆锥的表面积.
分析 (Ⅰ)证法1:设BC∩OD=E,由已知可证AC∥OE,线线平行即可证明线面平行AC∥平面POD;证法2:由AB是底面圆的直径,可证AC⊥BC,利用OD⊥BC,可证AC∥OD,即可判定AC∥平面POD.
(Ⅱ)设圆锥底面半径为r,高为h,母线长为l,由圆锥的轴截面PAB为等腰直角三角形,可求$h=r,l=\sqrt{2}r$,利用三角形面积公式可求r,进而可求此圆锥的表面积.
解答 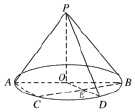 解:(Ⅰ)证法1:设BC∩OD=E,∵D是弧BC的中点,
解:(Ⅰ)证法1:设BC∩OD=E,∵D是弧BC的中点,
∴E是BC的中点,
又∵O是AB的中点,∴AC∥OE,
又∵AC?平面POD,OE?平面POD,
∴AC∥平面POD.
证法2:∵AB是底面圆的直径,∴AC⊥BC,
∵弧BC的中点为D,∴OD⊥BC,
又AC,OD共面,∴AC∥OD,
又AC?平面POD,OD?平面POD,
∴AC∥平面POD.
(Ⅱ)解:设圆锥底面半径为r,高为h,母线长为l,
∵圆锥的轴截面PAB为等腰直角三角形,
∴$h=r,l=\sqrt{2}r$,
∵由${S_{△ABC}}=\frac{1}{2}×2r×h={r^2}=9$,得r=3,
∴${S_表}=πrl+π{r^2}=πr×\sqrt{2}r+π{r^2}=9({1+\sqrt{2}})π$.
点评 本题主要考查了线面平行的判定,考查了三角形面积公式,考查了圆锥的表面积的求法,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
15.一种专门侵占内存的计算机病毒,开机时占据内存2KB,然后每3分钟自身复制一次,复制后所占内存是原来的2倍,若该病毒占据64MB内存(1MB=210KB),则开机后经过( )分钟.
| A. | 45 | B. | 44 | C. | 46 | D. | 47 |
12.如图给出的是计算$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+…+\frac{1}{18}$的值的一个程序框图,其中判断框内应填入的条件是( )


| A. | i>9 | B. | i<9 | C. | i>18 | D. | i<18 |
19.如图是用二分法求方程x3-2=0近似解的算法的程序框图,则①②两处应依次填入( )


| A. | a=m,b=m | B. | b=m,a=m | C. | a=f(m),b=f(m) | D. | b=f(m),a=f(m) |
9.执行如图的程序框图,则输出的S值为( )


| A. | 33 | B. | 215 | C. | 343 | D. | 1025 |
16.有两位射击运动员在一次射击测试中各射靶7次,每次命中的环数如下:
甲 7 8 10 9 8 8 6
乙 9 10 7 8 7 7 8
则下列判断正确的是( )
甲 7 8 10 9 8 8 6
乙 9 10 7 8 7 7 8
则下列判断正确的是( )
| A. | 甲射击的平均成绩比乙好 | |
| B. | 乙射击的平均成绩比甲好 | |
| C. | 甲射击的成绩的众数小于乙射击的成绩的众数 | |
| D. | 甲射击的成绩的极差大于乙射击的成绩的极差 |
14.已知a=sin153°,b=cos62°,$c={log_{\frac{1}{2}}}\frac{1}{3}$,则( )
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |