题目内容
16. 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,过两个焦点和一个顶点的三角形面积为1.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,过两个焦点和一个顶点的三角形面积为1.(1)求椭圆的方程;
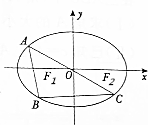
(2)如图,点A为椭圆上一动点(非长轴端点),AF1的延长线与椭圆交于B点,AO的延长线与椭圆交于C点,求△ABC面积的最大值,并求此时直线AB的方程.
分析 (1)根据题意,得出$\frac{b}{a}$=$\frac{\sqrt{2}}{2}$①,cb=1②,a2=b2+c2③,由①②③解得c、b、a的值即可;
(2)讨论直线AB的斜率不存在与斜率存在时,求出对应△ABC的面积,由此判断△ABC面积的最大值以及此时AB的直线方程.
解答 解:(1)椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)中,
过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,∴$\frac{b}{a}$=$\frac{\sqrt{2}}{2}$①;
过两个焦点和一个顶点的三角形面积为1,∴c•b=1②;
又a2=b2+c2③,
由①②③解得c=b=1,a=$\sqrt{2}$;
∴椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)当直线AB的斜率不存在时,
可知A(-1,$\frac{\sqrt{2}}{2}$),B(-1,-$\frac{\sqrt{2}}{2}$),C(1,-$\frac{\sqrt{2}}{2}$),
故S△ABC=$\sqrt{2}$,
当直线AB的斜率存在时,设直线AB的方程为y=k(x+1),
联立方程$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{x}^{2}}{2}{+y}^{2}=1}\end{array}\right.$化简得,
(2k2+1)x2+4k2x+2k2-2=0,
∴xA+xB=-$\frac{{4k}^{2}}{{2k}^{2}+1}$,xAxB=$\frac{{2k}^{2}-2}{{2k}^{2}+1}$,
故|xA-xB|=$\sqrt{{{(x}_{A}{+x}_{B})}^{2}-{{4x}_{A}x}_{B}}$
=2$\sqrt{2}$•$\frac{\sqrt{{k}^{2}+1}}{{2k}^{2}+1}$,
故|AB|=$\sqrt{1{+k}^{2}}$|xA-xB|
=2$\sqrt{2}$•$\frac{{k}^{2}+1}{{2k}^{2}+1}$,
点C到直线AB的距离d=$\frac{|k({-x}_{A}+1){+y}_{A}|}{\sqrt{{k}^{2}+1}}$=$\frac{2|k|}{\sqrt{{k}^{2}+1}}$,
故S△ABC=$\frac{1}{2}$•(2$\sqrt{2}$•$\frac{{k}^{2}+1}{{2k}^{2}+1}$)•$\frac{2|k|}{\sqrt{{k}^{2}+1}}$
=2$\sqrt{2}$•$\sqrt{\frac{{k}^{2}{(k}^{2}+1)}{{({2k}^{2}+1)}^{2}}}$
=2$\sqrt{2}$•$\sqrt{\frac{1}{4}-\frac{1}{{4({2k}^{2}+1)}^{2}}}$<$\sqrt{2}$;
综上,△ABC面积的最大值为$\sqrt{2}$,此时AB的方程为x+1=0.
点评 本题考查了椭圆与双曲线的性质应用,同时考查了数形结合的思想应用及分类讨论的思想应用,关键在于化简运算.

| A. | ${\overrightarrow e_1}$和 ${\overrightarrow e_1}$+${\overrightarrow e_2}$ | B. | ${\overrightarrow e_1}$-2${\overrightarrow e_2}$和${\overrightarrow e_1}$-${\overrightarrow e_2}$ | ||
| C. | ${\overrightarrow e_1}$+${\overrightarrow e_2}$和${\overrightarrow e_1}$-${\overrightarrow e_2}$ | D. | 2${\overrightarrow e_1}$-${\overrightarrow e_2}$和$\frac{1}{2}$${\overrightarrow e_2}$-${\overrightarrow e_1}$ |
| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
| A. | 1121(4) | B. | 1211(4) | C. | 1021(4) | D. | 1201(4) |
| A. | (-1,1) | B. | ($\frac{\sqrt{3}}{2}$,1) | C. | (-1,-$\frac{\sqrt{3}}{2}$] | D. | (-1,$\frac{\sqrt{3}}{2}$] |
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | $\frac{7}{4}$ |