题目内容
6.已知点A(2,1),P是焦点为F的抛物线y2=4x上的任一点,当△PAF的周长最小时,△PAF的面积为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{7}{8}$ | D. | $\frac{7}{4}$ |
分析 设点P在准线上的射影为D,则根据抛物线的定义可知|PF|=|PD|进而把问题转化为求|PA|+|PD|取得最小,推断出当D,P,A三点共线时|PA|+|PD|最小,求出P的坐标,可得△PAF的面积.
解答 解:设点P在准线上的射影为D,则根据抛物线的定义可知|PF|=|PD|
∴△APF的周长最小,|PA|+|PF|取得最小值,即求|PA|+|PD|取得最小
当D,P,A三点共线时|PA|+|PD|最小,设P(x,1),则1=4x,
∴x=$\frac{1}{4}$,
∴P($\frac{1}{4}$,1).
∴△PAF的面积为$\frac{1}{2}×(2-\frac{1}{4})×1$=$\frac{7}{8}$,
故选:C.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,属于中档题,正确转化是关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
1.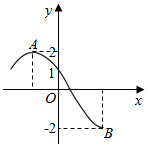 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
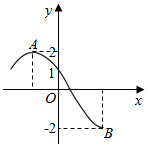 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=( )| A. | -1 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 1 |
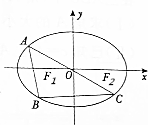 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,过两个焦点和一个顶点的三角形面积为1.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点F1,F2,过其中两个端点的直线斜率为$\frac{\sqrt{2}}{2}$,过两个焦点和一个顶点的三角形面积为1.