题目内容
已知函数f(x)=sin5x+1,则:∫
f(x)dx等于 .
-
|
考点:定积分
专题:导数的综合应用
分析:由和的积分等于积分的和展开,由定积分的几何意义可得
sin5xdx=0,然后直接求定积分
1dx得答案.
| ∫ |
-
|
| ∫ |
-
|
解答:
解:∫
f(x)dx
=
(sin5x+1)dx
=
sin5xdx
1dx.
∵函数y=sin5x为奇函数,∴其图象关于原点中心对称,
又积分区间关于原点对称,∴
sin5xdx=0.
则∫
f(x)dx=
1dx=x
=
-(-
)=π.
故答案为:π.
-
|
=
| ∫ |
-
|
=
| ∫ |
-
|
| +∫ |
-
|
∵函数y=sin5x为奇函数,∴其图象关于原点中心对称,
又积分区间关于原点对称,∴
| ∫ |
-
|
则∫
| ||
-
|
| ∫ |
-
|
| | |
-
|
| π |
| 2 |
| π |
| 2 |
故答案为:π.
点评:本题考查了定积分,考查了微积分基本定理,解答的关键是对定积分几何意义的理解,是中档题.

练习册系列答案
相关题目
函数f(x)=(sinx-cosx)•cosx的最小正周期为( )
| A、π | ||
B、
| ||
| C、2π | ||
D、
|
下列函数中是幂函数的是( )
| A、y=3x3 | ||
| B、y=(x-1)2 | ||
C、y=-
| ||
| D、y=xπ-1 |
在△ABC中,如果sinAsinB+sinAcosB+cosAsinB+cosAcosB=2,则△ABC是( )
| A、等边三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
已知不等式ax2-bx+1≥0的解集是[-1,2],则不等式x2-bx+a<0的解集是( )
A、(-
| ||
B、(-∞,-1)∪(
| ||
C、(-∞,-
| ||
D、(-1,
|
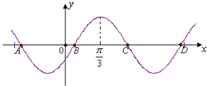 已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,点B(
已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,点B(