题目内容
已知sin(α+
)=
,则sin2α= .
| π |
| 4 |
| ||
| 3 |
考点:二倍角的正弦
专题:三角函数的求值
分析:首先利用两角和与差公式将已知条件展开,然后两边平方和sin2α+cos2α=1,得出2sinαcosα的值,从而由二倍角公式得出答案.
解答:
解:∵sin(α+
)=
(sinα+cosα)=
∴两边平方得,
(sin2α+2cosαsinα+cos2α)=
∴2sinαcosα=-
故sin2α=-
故答案为:-
| π |
| 4 |
| ||
| 2 |
| ||
| 3 |
∴两边平方得,
| 1 |
| 2 |
| 2 |
| 9 |
∴2sinαcosα=-
| 5 |
| 9 |
故sin2α=-
| 5 |
| 9 |
故答案为:-
| 5 |
| 9 |
点评:本题主要考查了两角和与差公式和二倍角公式,熟练掌握相关公式是解题的关键.

练习册系列答案
相关题目
在△ABC中,如果sinAsinB+sinAcosB+cosAsinB+cosAcosB=2,则△ABC是( )
| A、等边三角形 |
| B、钝角三角形 |
| C、等腰直角三角形 |
| D、直角三角形 |
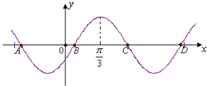 已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,点B(
已知函数f(x)=sin(ωx+φ)(ω>0)的部分图象如图所示,点B(