题目内容
18.某地为了抑制一种有害昆虫的繁殖,引入了一种以该昆虫为食物的特殊动物,已知该动物的繁殖数量y(只)与引入时间x(年)的关系为y=alog2(x+1),若该动物在引入一年后的数量为100只,则第7年它们发展到( )| A. | 300只 | B. | 400只 | C. | 600只 | D. | 700只 |
分析 将x=1,y=100代入y=alog2(x+1),得a=100,由此能求出结果.
解答 解:将x=1,y=100代入y=alog2(x+1)得,
100=alog2(1+1),
解得a=100,
所以x=7时,y=100log2(7+1)=300.
故选:A.
点评 本题考查函数在生产生活中的实际应用,是基础题,解题时要认真审题,注意对数函数性质的合理运用.

练习册系列答案
相关题目
8.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{2}$=1(a>0)的长轴长为4,则C的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{2}$ |
19.设命题 p:?n∈N,3n≥n2+1,则¬p为( )
| A. | ?n∈N,3n<n2+1 | B. | $?{n_0}∈N,{3^{n_0}}<n_0^2+1$ | ||
| C. | ?n∈N,3n≤n2+1 | D. | $?{n_0}∈N,{3^{n_0}}≥n_0^2+1$ |
20.如图,关于正方体ABCD-A1B1C1D1,下面结论错误的是( )


| A. | BD⊥平面ACC1A1 | |
| B. | AC⊥BD | |
| C. | A1B∥平面CDD1C1 | |
| D. | 该正方体的外接球和内接球的半径之比为2:1 |
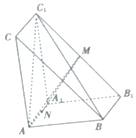 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点