题目内容

若sin（
π
3
-α）=
1
4
，则cos（
π
6
+α）=
 
．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：直接利用诱导公式把要求的式子化为sin（
π
3
-α），利用条件求得结果．
解答： 解：∵sin（
π
3
-α）=
1
4
，∴cos（
π
6
+α）=cos[
π
2
-（
π
3
-α）]=sin（
π
3
-α）=
1
4
，
故答案为：
1
4
．
点评：本题主要考查利用诱导公式进行化简求值，属于基础题．
练习册系列答案
相关题目
已知a，b，c∈R*，证明：
（1）（a+b+c）（a2+b2+c2）≤3（a3+b3+c3）；
（2）
a
b+c
+
b
c+a
+
c
a+b
≥
3
2
．
在△ABC中，角A，B，C的对边分别是a，b，c，若3sinB=2sinC，a2-b2=
5
2
bc，则A=
 
．
曲线y=xsinx在点A（
π
2
，
π
2
），B（-
π
2
，
π
2
））处的切线分别为l1，l2，设l1，l2及直线x-2y+2=0围成的区域为D（包括边界）．设点P（x，y）是区域D内任意一点，则x+2y的最大值为
 
．
对于定义在R上的函数f（x）图象连续不断，若存在常数a（a∈R），使得f（x+a）+af（x）=0对任意的实数x成立，则称f （x）是阶数为a的回旋函数，现有下列4个命题：
①f（x）=x2必定不是回旋函数；
②若f（x）=sinωx（ω≠0）为回旋函数，则其最小正周期必不大于2；
③若指数函数为回旋函数，则其阶数必大于1；
④若对任意一个阶数为a（a≥0）的回旋函数f （x），方程f（x）=0均有实数根，其中为真命题的是
 
．
已知直线l与函数y=x2的图象交于A，B两点，且线段AB与函数y=x2的图象围成的图形面积为
4
3
，则线段AB的中点P的轨迹方程为
 
．
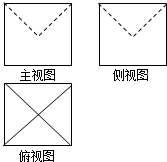某几何体的三视图如图所示，图中的四边形都是边长为1的正方形，两条虚线互相垂直，则该几何体的体积是（　　）
A、
1
6
B、
1
2
C、
5
6
D、1
已知复数z1=（2-i）i，复数z2=a+3i（a∈R），若复数z2=kz1（k∈R），则a=（　　）
A、
3
2
B、
2
3
C、
1
2
D、
1
3
已知sinx-cosx=-
2
，则tanx=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网