题目内容
一个含有10项的数列{an}满足：a1=0，a10=5，|ak+1-ak|=1，（k=1，2，…，9），则符合这样条件的数列{an}有（ ）个．
| A、30 | B、35 | C、36 | D、40 |
考点：排列、组合的实际应用,数列的概念及简单表示法
专题：计算题,数学模型法,排列组合
分析：结合数列的函数特征，将数列{an}看成点（n，an），在直角坐标系下表示出来，可将原问题可转化为在平面直角坐标系中，由（1，0）点走9步到达（10，5）点，每步需向右移1个单位，同时向上（下）移1个单位；由组合数公式分析可得答案．
解答：
解：将数列{an}看成点（n，an），在直角坐标系下表示出来，
则原问题可转化为在平面直角坐标系中，由（1，0）点走9步到达（10，5）点，
每步需向右移1个单位，同时向上（下）移1个单位，
分析可得，9步中有且只有2步向下移1个单位，7步向上移动，
则不同的走法有C92=36，
故选C．
解：将数列{an}看成点（n，an），在直角坐标系下表示出来，则原问题可转化为在平面直角坐标系中，由（1，0）点走9步到达（10，5）点，
每步需向右移1个单位，同时向上（下）移1个单位，
分析可得，9步中有且只有2步向下移1个单位，7步向上移动，
则不同的走法有C92=36，
故选C．
点评：本题考查排列、组合的应用，关键是将原问题转化为排列、组合的问题．
练习册系列答案
科学实验活动册系列答案
相关题目
在平面上有一个长为12cm，宽为10cm的矩形，现把一个半径为1cm的硬币任意投掷在矩形内，则硬币不与矩形相碰的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线y=x3-2x+4在点（1，3）处的切线方程为（ ）
| A、3x-y=0 |
| B、x+y-4=0 |
| C、x-y+2=0 |
| D、x-y-2=0 |
复数z=
的共轭复数是（ ）
| i |
| 1+i |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
将角-
π写成α+2kπ（k∈Z，0≤α＜2π）的形式，正确的是（ ）
| 27 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
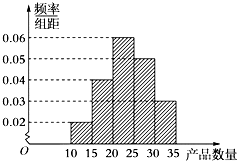为了调查某厂2000名工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量，产品数量的分组区间为[10，15），[15，20），[20，25），[25，30），[30，35]，频率分布直方图如图所示．工厂规定从生产低于20件产品的工人中随机地选取2位工人进行培训，则这2位工人不在同一组的概率是（ ）