题目内容
4．已知集合A={x|1＜x＜3}，集合B={x|2m＜x＜1-m}．（1）若m=-1求A∩B；
（2）若A∩B=∅，求实数m的取值范围．
分析 （1）根据交集的定义即可求出，
（2）分类讨论，即可求出m的范围．
解答 解：（1）m=-1时，集合B={x|-2＜x＜2}．
∵A={x|1＜x＜3}，
∴A∩B={x|1＜x＜2}，
（2）若A∩B=∅，得
①若2m≥1-m，即$m≥\frac{1}{3}$时，B=∅，符合题意；
②若2m＜1-m，即$m＜\frac{1}{3}$时，需$\left\{\begin{array}{l}m＜\frac{1}{3}\\ 1-m≤1\end{array}\right.$或$\left\{\begin{array}{l}m＜\frac{1}{3}\\ 2m≥3\end{array}\right.$
得$0≤m＜\frac{1}{3}$或∅，即$0≤m＜\frac{1}{3}$．
综上知m≥0
点评 本题考查了交集的运算，关键是分类讨论，属于基础题．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
课程达标测试卷闯关100分系列答案
相关题目
15．已知变量x，y满足约束条件$\left\{\begin{array}{l}{x+y≤3}&{\;}\\{x-y≤2}&{\;}\\{x≥1}&{\;}\end{array}\right.$，若x+2y≥a恒成立，则实数a的取值范围为（ ）
| A． | （-∞，-1] | B． | （-∞，2] | C． | （-∞，3] | D． | [-1，3] |
12．在正方体ABCD-A1B1C1D1中AD1与BD所成的角为（ ）
| A． | 45° | B． | 90° | C． | 60° | D． | 120° |
19．
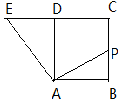如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若点P为BC的中点，且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$，则λ+μ=（ ）
如图，四边形ABCD是正方形，延长CD至E，使得DE=CD，若点P为BC的中点，且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$，则λ+μ=（ ）| A． | 3 | B． | 2 | C． | 1 | D． | $\frac{5}{2}$ |