题目内容
15.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤3}&{\;}\\{x-y≤2}&{\;}\\{x≥1}&{\;}\end{array}\right.$,若x+2y≥a恒成立,则实数a的取值范围为( )| A. | (-∞,-1] | B. | (-∞,2] | C. | (-∞,3] | D. | [-1,3] |
分析 要使x+2y≥a恒成立,需使x+2y得最小值大于等于a,设z=x+2y,可得y=-$\frac{1}{2}$x+z,即z为平行直线的斜率,作出足约束条件$\left\{\begin{array}{l}{x+y≤3}&{\;}\\{x-y≤2}&{\;}\\{x≥1}&{\;}\end{array}\right.$,对应的可行域,平移直线可得最小值,可得答案.
解答 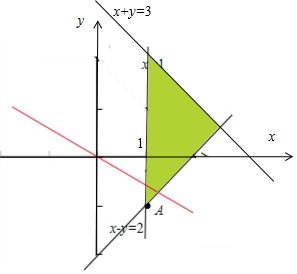 解:要使x+2y≥a恒成立,需使x+2y得最小值大于等于a,
解:要使x+2y≥a恒成立,需使x+2y得最小值大于等于a,
设z=x+2y,可得y=-$\frac{1}{2}$x+z,即z为平行直线的斜率,
作出足约束条件$\left\{\begin{array}{l}{x+y≤3}&{\;}\\{x-y≤2}&{\;}\\{x≥1}&{\;}\end{array}\right.$对应的可行域,如图:
平移直线可得当直线经过点A(1,-1)时,z取最小值-1,
故可得实数a的取值范围为a≤-1,
故选:A.
点评 本题考查简单的线性规划,准确作图时解决问题的关键,属中档题.

练习册系列答案
相关题目
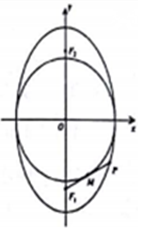 若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M.
若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M.