题目内容
3.把复数z的共轭复数记作$\overline z$,已知$(1+2i)\overline z=4+3i$,求z及$\frac{z}{\overline z}$.分析 (1)把已知等式变形,利用复数代数形式的乘除运算化简求得z;
(2)把z与$\overline{z}$代入$\frac{z}{\overline z}$,再由复数代数形式的乘除运算化简得答案.
解答 解:(1)由$(1+2i)\overline z=4+3i$,得:
$\overline{z}$=$\frac{4+3i}{1+2i}$=$\frac{(4+3i)(1-2i)}{(1+2i)(1-2i)}=\frac{10-5i}{5}=2-i$,
∴$z=\overline{\overline{z}}=2+i$;
(2)$\frac{z}{\overline{z}}$=$\frac{2+i}{2-i}=\frac{(2+i)^{2}}{(2-i)(2+i)}=\frac{3}{5}+\frac{4}{5}i$.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
14.已知定义在R上的函数$f(x)=\frac{1}{3}a{x^3}+{x^2}+ax+1$既有极大值又有极小值,则实数a的取值范围是( )
| A. | (-∞,-1)∪(1,+∞) | B. | [-1,0)∪(0,1] | C. | (-1,1) | D. | (-1,0)∪(0,1) |
11.k>3是方程$\frac{x^2}{k-3}-\frac{y^2}{k+3}=1$表示双曲线的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
18.设实数x和y满足约束条件$\left\{\begin{array}{l}{x+y≤10}\\{x-y≤2}\\{x≥4}\end{array}\right.$,则z=2x+3y的最大值为( )
| A. | 26 | B. | 24 | C. | 16 | D. | 14 |
19.如图(1),五边形PABCD是由一个正方形与一个等腰三角形拼接而成,其中∠APD=120°,AB=2,现将△PAD进行翻折,使得平面PAD⊥平面ABCD,连接PB,PC,所得四棱锥P-ABCD如图(2)所示,则四棱锥P-ABCD的外接球的表面积为( )
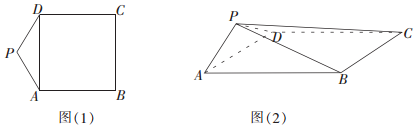

| A. | $\frac{14}{3}π$ | B. | $\frac{7}{3}π$ | C. | $\frac{28}{3}π$ | D. | 14π |