Question

12．若直角坐标平面内两点P，Q满足条件：①P，Q都在函数y=f（x）的图象上；②P，Q关于原点对称，则称（P，Q）是函数y=f（x）的一个“伙伴点组”（点组（P，Q）与（Q，P）看作同一个“伙伴点组”）．已知函数$f（x）=\left\{\begin{array}{l}kx-1，x＞0\\-ln（-x），x＜0\end{array}\right.$，有两个“伙伴点组”，则实数k的取值范围是（　　）

• A． （-∞，0）
• B． （0，1）
• C． （0，$\frac{1}{2}$）
• D． （0，+∞）

Answer 1

分析 可作出函数y=-ln（-x）（x＜0）关于原点对称的函数y=lnx（x＞0）的图象，使它与函数y=kx-1（x＞0）交点个数为2个即可．通过直线绕着（0，-1）旋转，求得与y=lnx相切的情况，再由图象观察即可得到所求k的范围．

解答 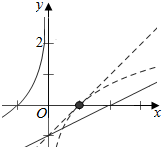解：根据题意可知，“伙伴点组”满足两点：
都在函数图象上，且关于坐标原点对称．
可作出函数y=-ln（-x）（x＜0）
关于原点对称的函数y=lnx（x＞0）的图象，
使它与函数y=kx-1（x＞0）交点个数为2个即可． 
设切点为（m，lnm），y=lnx的导数为y′=$\frac{1}{x}$，
可得km-1=lnm，k=$\frac{1}{m}$，解得m=1，k=1，
可得函数y=lnx（x＞0）过（0，-1）点的切线斜率为1，
结合图象可知k∈（0，1）时有两个交点．
故选B．

点评 本题考查新定义的理解和运用，考查导数的运用：求切线的斜率，考查数形结合的思想方法，属于中档题．