题目内容
6.若以不等式log${\;}_{\frac{1}{2}}$(x2-x-2)<log${\;}_{\frac{1}{2}}$(x-1)-1的解集为定义域,求函数y=4x-2x+1+5的值域.分析 把不等式log${\;}_{\frac{1}{2}}$(x2-x-2)<log${\;}_{\frac{1}{2}}$(x-1)-1化为等价的不等式组,求出解集,即得函数y的定义域,再求函数y的值域即可.
解答 解:不等式log${\;}_{\frac{1}{2}}$(x2-x-2)<log${\;}_{\frac{1}{2}}$(x-1)-1可化为
log${\;}_{\frac{1}{2}}$(x2-x-2)<log${\;}_{\frac{1}{2}}$2(x-1),
即$\left\{\begin{array}{l}{{x}^{2}-x-2>2(x-1)}\\{x-1>0}\end{array}\right.$,
化简得$\left\{\begin{array}{l}{{x}^{2}-3x>0}\\{x>1}\end{array}\right.$,
解得x>3;
∴该不等式的解集为(3,+∞);
又当x∈(3,+∞)时,
函数y=4x-2x+1+5=22x-2•2x+5=(2x-1)2+4是单调增函数,
∴y>22×3-2•23+5=53;
∴函数y的值域为(53,+∞).
点评 本题考查了指数函数与对数函数的定义域和值域的应用问题,解题时要注意指数与对数的性质的合理运用,是基础题目.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
12.若直角坐标平面内两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称(P,Q)是函数y=f(x)的一个“伙伴点组”(点组(P,Q)与(Q,P)看作同一个“伙伴点组”).已知函数$f(x)=\left\{\begin{array}{l}kx-1,x>0\\-ln(-x),x<0\end{array}\right.$,有两个“伙伴点组”,则实数k的取值范围是( )
| A. | (-∞,0) | B. | (0,1) | C. | (0,$\frac{1}{2}$) | D. | (0,+∞) |
10.已知f(x)=$\frac{{2}^{x+1}+1}{{2}^{x}-1}$,且对于任意x∈[1,3],不等式f(x)>|x-2|+m恒成立,则m的取值范围是( )
| A. | (-∞,-4] | B. | (-$\frac{1}{2}$,+∞) | C. | (-∞,-$\frac{9}{8}$) | D. | (-∞,$\frac{10}{7}$) |
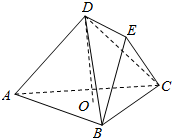 如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.
如图所示,在几何体ABCDE中,AB=BC=CA=EB=EC=2$\sqrt{3}$,DE=$\sqrt{2}$,点D在底面ABC上的射影O为底面三角形ABC的中心,平面BEC⊥平面ABC.