题目内容
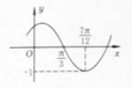 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式,再根据y=Asin(ωx+φ)的图象变换规律,可得结论.
解答:
解:由函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
)的图象可得
A=1,
=
•
=
-
,求得ω=2.
再根据五点法作图可得2×
+φ=π,求得φ=
,
函数f(x)=sin(2x+
).
故把f(x)的图象向右平移
个单位长度,可得函数g(x)=sin2(x-
)+
]=sin2x的图象,
故选:A.
| π |
| 2 |
A=1,
| T |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
再根据五点法作图可得2×
| π |
| 3 |
| π |
| 3 |
函数f(x)=sin(2x+
| π |
| 3 |
故把f(x)的图象向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
故选:A.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
已知函数f(x)的定义域为[
,4],则函数g(x)=
+f(2x)的定义域为( )
| 1 |
| 4 |
| 1 |
| ln(x+1) |
| A、[-2,0)∪(0,2] |
| B、(-1,0)∪(0,2] |
| C、[-2,2] |
| D、(-1,2] |
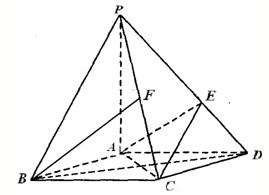 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=