题目内容
8．
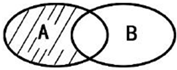已知不等式|x-2|＜3的解集为 A，函数y=ln（1-x）的定义域为B，则图中阴影部分表示的集合为{x|1≤x＜5}．
分析 由韦恩图中阴影部分表示的集合为A∩（∁RB），然后利用集合的基本运算进行求解即可．
解答 解：A={x||x-2|＜3}={x|-1＜x＜5}，B={x|y=ln（1-x）}={x|1-x＞0}={x|x＜1}，
则∁UB={x|x≥1}，
由韦恩图中阴影部分表示的集合为A∩（∁UB），
∴A∩（∁UB）={x|1≤x＜5}，
故答案为：{x|1≤x＜5}．
点评 本题主要考查集合的基本运算，利用韦恩图确定集合关系，然后利用数轴求基本运算是解决此类问题的基本方法．
练习册系列答案
相关题目
16．世园会期间，某班有四名学生参加了志愿工作．将这四名学生分配到A，B，C三个不同的展馆服务，每个展馆至少分配一人．则四人中学生甲不到A馆的概率为（ ）
| A． | 1 | B． | $\frac{5}{6}$ | C． | $\frac{2}{3}$ | D． | $\frac{5}{9}$ |
13．已知集合A={y|y=$\sqrt{2-x}$}，B={x|x2-2x＞0}，则（ ）
| A． | A∩B=∅ | B． | A∪B=R | C． | B⊆A | D． | A⊆B |
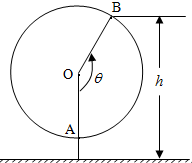如图为一个观览车示意图．该观览车圆半径为5米，圆上最低点与地面距离为1米，60秒转动一圈．图中OA与地面垂直．设从OA开始转动，逆时针转动θ角到OB．设B点与地面距离为h．