题目内容
7.已知函数f(x)=$\frac{x}{a}-{e^x}$(a>0)(Ⅰ)求函数f(x)在[1,2]上的最大值;
(Ⅱ)若函数f(x)有2个零点,求实数a的取值范围.
分析 (I)$f'(x)=\frac{1}{a}-{e^x}$,令f′(x)=0,则$x=ln\frac{1}{a}$.对ln$\frac{1}{a}$与1,2的大小关系分类讨论即可得出.
(Ⅱ)令$f(x)=\frac{x}{a}-{e^x}=0$,则$a=\frac{x}{e^x}$.问题转化为y=a与函数$g(x)=\frac{x}{e^x}$有2个交点.利用导数研究函数g(x)的单调性极值与最值即可得出.
解答 解:(I)$f'(x)=\frac{1}{a}-{e^x}$,令f′(x)=0,则$x=ln\frac{1}{a}$.
当$ln\frac{1}{a}≥2$,即$0<a≤\frac{1}{e^2}$,f(x)在[1,2]上单调递增,∴$f{(x)_{max}}=f(2)=\frac{2}{a}-{e^2}$;
当$1<ln\frac{1}{a}<2$,即$\frac{1}{e^2}<a<\frac{1}{e}$,f(x)在$[{1,ln\frac{1}{a}}]$上单调递增,在$[{ln\frac{1}{a},2}]$上单调递减,
∴$f{(x)_{max}}=f({ln\frac{1}{a}})=\frac{1}{a}ln\frac{1}{a}-\frac{1}{a}$;
当$ln\frac{1}{a}≤1$,即$a≥\frac{1}{e}$,f(x)在[1,2]上单调递减,∴$f{(x)_{max}}=f(1)=\frac{1}{a}-e$.
(Ⅱ)令$f(x)=\frac{x}{a}-{e^x}=0$,则$a=\frac{x}{e^x}$.
问题转化为y=a与函数$g(x)=\frac{x}{e^x}$有2个交点.
令$g'(x)=\frac{1-x}{e^x}=0$,则x=1.
当x<1时,g'(x)>0,当x>1时,g'(x)<0.
∴当x=1时,g(x)取得极大值也为最大值$g(1)=\frac{1}{e}$.
且x→+∞,g(x)→0;x→-∞,g(x)→-∞.
故$a∈({0,\frac{1}{e}})$时,y=a与函数$g(x)=\frac{x}{e^x}$有2个交点,
即函数f(x)有2个零点.
点评 本题考查了利用导数研究函数的单调性极值与最值、不等式的解法,考查了分类讨论方法、推理能力与计算能力,属于难题.

| A. | 0 | B. | $\frac{π}{4}$ | C. | 2 | D. | 4 |
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
| A. | 1 | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
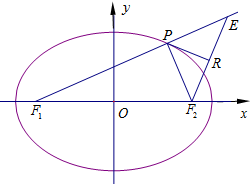 已知F1,F2分别为椭圆的左、右两个焦点,椭圆的离心率为$\frac{\sqrt{6}}{3}$,短轴的一个端点到一个焦点的距离为$\sqrt{3}$.设点P是椭圆上的动点,过点F2作∠F1PF2的外角平分线PR的垂线,交F1P的延长线于E,垂足为R.
已知F1,F2分别为椭圆的左、右两个焦点,椭圆的离心率为$\frac{\sqrt{6}}{3}$,短轴的一个端点到一个焦点的距离为$\sqrt{3}$.设点P是椭圆上的动点,过点F2作∠F1PF2的外角平分线PR的垂线,交F1P的延长线于E,垂足为R.