题目内容
6.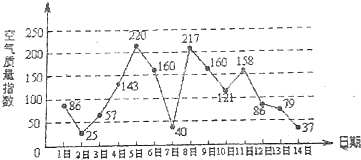 如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
如图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.(Ⅰ)求此人到达当日空气重度污染的概率.
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
分析 (Ⅰ)设Ai表示“此人于3月i日到达该市”,(i=1,2,…,13),根据题意,P(Ai)=$\frac{1}{13}$,且Ai∩j=∅(i≠j),设B为事件“此人到达当日空气重度污染”,则B=A5∪A8,由此能求出此人到达当日空气重度污染的概率.
(Ⅱ)由题意知X的所有可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解::(Ⅰ)设Ai表示“此人于3月i日到达该市”,(i=1,2,…,13),
根据题意,P(Ai)=$\frac{1}{13}$,且Ai∩j=∅(i≠j),
设B为事件“此人到达当日空气重度污染”,则B=A5∪A8,
∴此人到达当日空气重度污染的概率:
P(B)=P(A5)+P(A8)=$\frac{1}{13}$+$\frac{1}{13}$=$\frac{2}{13}$.
(Ⅱ)由题意知X的所有可能取值为0,1,2,
P(X=1)=P(A3∪A6∪A7∪A11)=$\frac{4}{13}$,
P(X=2)=P(A1∪A2∪A12∪A13)=$\frac{4}{13}$,
P(X=0)=1-P(X=1)-P(X=2)=$\frac{5}{13}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{5}{13}$ | $\frac{4}{13}$ | $\frac{4}{13}$ |
点评 本题考查了离散型随机变量的概率计算及其分布列、数学期望、古典概率计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.世园会期间,某班有四名学生参加了志愿工作.将这四名学生分配到A,B,C三个不同的展馆服务,每个展馆至少分配一人.则四人中学生甲不到A馆的概率为( )
| A. | 1 | B. | $\frac{5}{6}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
15.已知角α的终边经过点P(-1,1),则cosα的值为( )
| A. | 1 | B. | -1 | C. | -$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
6.在极坐标系中,圆心在($\sqrt{2}$,π)且过极点的圆的方程为( )
| A. | ρ=2$\sqrt{2}$cos θ | B. | ρ=-2$\sqrt{2}$cos θ | C. | ρ=2$\sqrt{2}$sin θ | D. | ρ=-2$\sqrt{2}$sin θ |
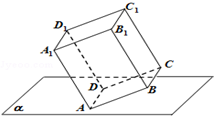 长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.
长方体ABCD-A1B1C1D1中,已知AA1=3,AB=AD=2,棱AD在平面α内,则长方体在平面α内的射影所构成的图形面积的取值范围是$4≤S≤2\sqrt{13}$.