题目内容
18.已知|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°(1)若$\overrightarrow{a}$⊥($\overrightarrow{a}$+k$\overrightarrow{b}$),求k的值;
(2)求|$\overrightarrow{a}$+2$\overrightarrow{b}$|的值.
分析 (1)令$\overrightarrow{a}$•($\overrightarrow{a}$+k$\overrightarrow{b}$)=0解出k;
(2)求出|$\overrightarrow{a}$+2$\overrightarrow{b}$|2,然后开方即可.
解答 解:(1)$\overrightarrow{a}•\overrightarrow{b}$=4×3×cos120°=-6.
∵$\overrightarrow{a}$⊥($\overrightarrow{a}$+k$\overrightarrow{b}$),
∴$\overrightarrow{a}$•($\overrightarrow{a}$+k$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$+k$\overrightarrow{a}•\overrightarrow{b}$=0,即16-6k=0,
解得k=$\frac{8}{3}$.
(2)($\overrightarrow{a}+2\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}$=16-24+36=28.
∴|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{28}=2\sqrt{7}$.
点评 本题考查了平面向量的数量级运算,属于基础题.

练习册系列答案
相关题目
8.如图,已知直线y=kx+m与曲线y=f(x)相切于两点,则F(x)=f(x)-kx有( )
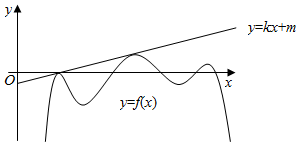

| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
9.对于锐角α,若sin(α-$\frac{π}{6}$)=$\frac{1}{3}$,则cos(α-$\frac{π}{3}$)=( )
| A. | $\frac{2\sqrt{6}+1}{6}$ | B. | $\frac{3-\sqrt{2}}{8}$ | C. | $\frac{3+\sqrt{2}}{8}$ | D. | $\frac{2\sqrt{3}-1}{6}$ |
9.设双曲线$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1的一条渐近线为y=-2x,且一个焦点与抛物线x2=4y的焦点相同,则此双曲线的方程为( )
| A. | $\frac{5}{4}$x2-5y2=1 | B. | 5y2-$\frac{5}{4}$x2=1 | C. | $\frac{5}{4}$y2-5x2=1 | D. | 5x2-$\frac{5}{4}$y2=1 |