题目内容
17.设f(x)=(x2+x-1)9(2x+1)6,试求f(x)的展开式中:(1)所有项的系数和;
(2)所有偶次项的系数和及所有奇次项的系数和.
分析 (1)设 f(x)=(x2+x-1)9(2x+1)6 =a0+a1x+a2x2+a3x3+a4x4+…+a24x24,令x=1,可得所有项的系数和.
(2)再令x=-1,可得所有奇次项的系数和减去偶次项的系数和的值,再结合(1)的结果,求得所有偶次项的系数和及所有奇次项的系数和.
解答 解:(1)设 f(x)=(x2+x-1)9(2x+1)6 =a0+a1x+a2x2+a3x3+a4x4+…+a24x24,
令x=1,可得所有项的系数和为 a0+a1+a2 +a3 +a4 +…+a24=36=729 ①,即所有项的系数和为729.
(2)再令x=-1,可得 a0 -a1+a2 -a3 +a4 +…+a22-a23+a24=-1 ②,
由①②求得偶次项的系数和为 a0+a2 +a4 +…+a24=364,所有奇次项的系数和为 a1 +a3 +a5 +…+a23=365.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.如图,已知直线y=kx+m与曲线y=f(x)相切于两点,则F(x)=f(x)-kx有( )
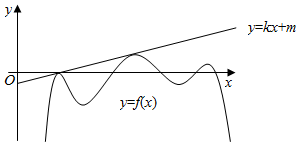

| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
5.若θ是第三象限角,且$\sqrt{1+sinθ}$=cos$\frac{θ}{2}$+sin$\frac{θ}{2}$,则$\frac{θ}{2}$是( )
| A. | 第二、四象限 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
2.已知多项式x2+x10=a0+a1(x+1)+a2(x+1)2+…+a9(x+1)9+a10(x+1)10,则a2=( )
| A. | 32 | B. | 42 | C. | 46 | D. | 56 |
9.对于锐角α,若sin(α-$\frac{π}{6}$)=$\frac{1}{3}$,则cos(α-$\frac{π}{3}$)=( )
| A. | $\frac{2\sqrt{6}+1}{6}$ | B. | $\frac{3-\sqrt{2}}{8}$ | C. | $\frac{3+\sqrt{2}}{8}$ | D. | $\frac{2\sqrt{3}-1}{6}$ |
9.设双曲线$\frac{{x}^{2}}{a}$+$\frac{{y}^{2}}{b}$=1的一条渐近线为y=-2x,且一个焦点与抛物线x2=4y的焦点相同,则此双曲线的方程为( )
| A. | $\frac{5}{4}$x2-5y2=1 | B. | 5y2-$\frac{5}{4}$x2=1 | C. | $\frac{5}{4}$y2-5x2=1 | D. | 5x2-$\frac{5}{4}$y2=1 |