题目内容
20.已知ω>0,函数f(x)=sin(ωx+$\frac{5π}{6}$)的一条对称轴为直线x=$\frac{π}{3}$,一个对称中心是($\frac{π}{12}$,0),则ω有( )| A. | 最小值2 | B. | 最大值2 | C. | 最小值1 | D. | 最大值1 |
分析 由条件利用正弦函数的图象的对称性,可得$\frac{1}{4}$•$\frac{2π}{ω}$≤$\frac{π}{3}$-$\frac{π}{12}$,求得ω≥2,从而得出结论.
解答 解:∵函数f(x)=sin(ωx+$\frac{5π}{6}$)的一条对称轴为直线x=$\frac{π}{3}$,一个对称中心是($\frac{π}{12}$,0),
∴$\frac{1}{4}$•$\frac{2π}{ω}$≤$\frac{π}{3}$-$\frac{π}{12}$,则ω≥2,故ω有最小值,
故选:A.
点评 本题主要考查正弦函数的图象的对称性,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.如图,已知直线y=kx+m与曲线y=f(x)相切于两点,则F(x)=f(x)-kx有( )
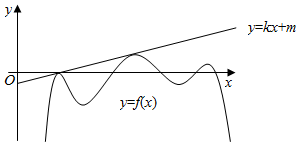

| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
5.若θ是第三象限角,且$\sqrt{1+sinθ}$=cos$\frac{θ}{2}$+sin$\frac{θ}{2}$,则$\frac{θ}{2}$是( )
| A. | 第二、四象限 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
9.对于锐角α,若sin(α-$\frac{π}{6}$)=$\frac{1}{3}$,则cos(α-$\frac{π}{3}$)=( )
| A. | $\frac{2\sqrt{6}+1}{6}$ | B. | $\frac{3-\sqrt{2}}{8}$ | C. | $\frac{3+\sqrt{2}}{8}$ | D. | $\frac{2\sqrt{3}-1}{6}$ |