题目内容
17.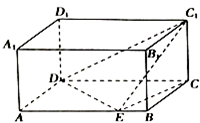 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.
分析 过点C作CF⊥DE于F,连结C1F,说明∠C1FC就是二面角C-DE-C1的平面角,在△C1FC中,∠C1CF=90°,求解tan∠C1FC的值即可.
解答 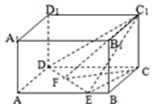 解:过点C作CF⊥DE于F,连结C1F,因为DE⊥C1C,所以DE⊥平面C1CF,所以C1F⊥DE,
解:过点C作CF⊥DE于F,连结C1F,因为DE⊥C1C,所以DE⊥平面C1CF,所以C1F⊥DE,
所以∠C1FC就是二面角C-DE-C1的平面角,
在△C1FC中,∠C1CF=90°,CF=CDsin45$°=2\sqrt{2}$.
所以tan∠C1FC=$\frac{C{C}_{1}}{CF}$=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查二面角的平面角的求法,考查空间想象能力以及计算能力,转化思想的应用.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
6.已知$f(x)=sin[\frac{π}{3}(x+1)]-\sqrt{3}cos[\frac{π}{3}(x+1)]$,则f(1)+f(2)+f(3)+…+f(2013)=( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
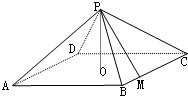 如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,
如图:四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,AB=2,∠BAD=$\frac{π}{3}$,M是BC上的点,且BM=$\frac{1}{2}$,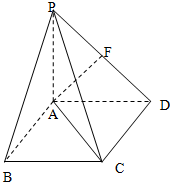 如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,PA=AD,F为PD的中点.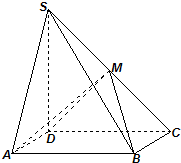 如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.
如图,四棱锥S-ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD=$\sqrt{2}$,DC=SD=2,点M是侧棱SC的中点.