题目内容
6.已知$f(x)=sin[\frac{π}{3}(x+1)]-\sqrt{3}cos[\frac{π}{3}(x+1)]$,则f(1)+f(2)+f(3)+…+f(2013)=( )| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -2$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 利用辅助角公式将将函数化简,根据三角函数是周期性函数,找出f(1),f(2),f(3)…的关系,可得答案.
解答 解:已知$f(x)=sin[\frac{π}{3}(x+1)]-\sqrt{3}cos[\frac{π}{3}(x+1)]$=2sin($\frac{π}{3}x$),
周期T=$\frac{2π}{\frac{π}{3}}=6$
∴f(x)以6为周期的周期函数,
当x=1时,f(1)=2sin$\frac{π}{3}$=$\sqrt{3}$,
当x=2时,f(2)=2sin$\frac{2π}{3}$=$\sqrt{3}$,
当x=3时,f(3)=2sinπ=0,
当x=4时,f(4)=2sin$\frac{4π}{3}$=$-\sqrt{3}$,
当x=5时,f(5)=2sin$\frac{5π}{3}$=$-\sqrt{3}$
当x=6时,f(6)=2sinπ=0,
f(1)+f(2)+f(3)+…+f(2013)=335[f(1)+f(2)+f(3)+f(4)+f(5)+f(6)]+f(1)+f(2)+f(3)
=335×0+f(1)+f(2)+f(3)
=2$\sqrt{3}$.
故选D.
点评 本题考察了三角函数的化简能力和周期的计算.属于中档题.

练习册系列答案
相关题目
16.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此做了四次试验,得到的数据如下:
已知y关于x的回归方程y=bx+1.05,则b=0.7.
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
14.在△ABC中,AB=5,BC=2,∠B=60°,则$\overrightarrow{AB}$•$\overrightarrow{AC}$的值为( )
| A. | 5$\sqrt{3}$ | B. | 5 | C. | -5$\sqrt{3}$ | D. | 20 |
18.设a、b为正数,$\frac{1}{a}$+$\frac{1}{b}$≤2$\sqrt{2}$,(a-b)2=4(ab)3,则a+b=( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
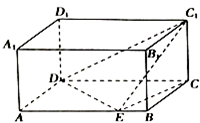 如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.
如图,在长方体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=2,E是线段AB上的点,且EB=1,则二面角C-DE-C1的正切值为$\frac{\sqrt{2}}{2}$.