题目内容
8.已知函数f(x)=ex-$\frac{1}{2}$kx2-2x+2,f′(x)是的导函数.(1)求f′(x)的单调区间;
(2)若k=1,证明:当x>0时,f(x)>0.
分析 (1)首先对f(x)求导,f'(x)=ex-kx-2,设g(x)=f'(x),则有g'(x)=ex-k;再对k分类讨论,判断函数单调区间;
(2)若k=1,由(I)知g(x)在(0,+∞)上递增,存在x0∈(1,2),使得g(x0)=0;
解答 解:(I)f'(x)=ex-kx-2,设g(x)=f'(x),则有g'(x)=ex-k;
①当k≤0时,g'(x)>0;
②当k>0时,由g'(x)>0得,x>lnk;
由g'(x)<0得,x<lnk.
当k≤0时,f'(x)的递增区间为R;
当k>0时,f'(x)的递增区间为(lnk,+∞),递减区间为(-∞,lnk).
(II)证明:若k=1,由(I)知g(x)在(0,+∞)上递增,
g(1)=e-3<0,g(2)=e2-4>0,
∴存在x0∈(1,2),使得g(x0)=0;
且当x>x0,g(x)>0,当x<x0时,g(x)<0;
∴f(x)的递增区间为(x0,+∞),递减区间为(0,x0),
∴f(x)≥f(x0)=${e}^{{x}_{0}}-\frac{1}{2}{x}_{0}^{2}-2{x}_{0}+2$;
由g(x0)=0得${e}^{{x}_{0}}$=x0+2,∴f(x0)=-$\frac{1}{2}{x}_{0}^{2}-{x}_{0}+4$
由x0∈(1,2)得f(x0)>0,
∴f(x)>0.
点评 本题主要考查了利用导数判断函数单调性,以及分类讨论思想应用,属中等题.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
16.已知点P在抛物线y2=4x上,则点P到直线l1:4x-3y+11=0的距离和到l2:x=-1的距离之和的最小值为( )
| A. | $\frac{37}{16}$ | B. | 3 | C. | 2 | D. | $\frac{11}{5}$ |
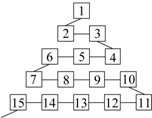 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第7个数是2010.
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行;数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;依此类推,则第63行从左至右的第7个数是2010.