题目内容
3.已知函数f(x)是定义在区间[-2,2]的奇函数,若f(x)+x•f′(x)>0,则不等式(-x+1)•f(1-x)>0的解集是[-1,1).分析 构造函数,设g(x)=xf(x),求导,根据题意得到函数g(x)为增函数,则求出g(0)=0,则不等式(-x+1)•f(1-x)>0转化为g(-x+1)>g(0),根据函数的单调性和函数的定义域即可求出不等式的解集.
解答 解:设g(x)=xf(x),
∴g′(x)=f(x)+x•f′(x)>0,
∴g(x)在[-2,2]上为增函数,
∵函数f(x)是定义在区间[-2,2]的奇函数,
∴g(0)=0×f(0)=0
∵(-x+1)•f(1-x)>0
∴g(-x+1)>g(0)
∴$\left\{\begin{array}{l}{-2≤-x+1≤2}\\{-x+1>0}\end{array}\right.$,
解得-1≤x<1,
故不等式的解集为[-1,1),
故答案为[-1,1).
点评 本题考查了导数和函数的单调性的应关系,以及不等式的解集的求法,关键是构造函数,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14.设函数f(x)=ex(sinx-cosx)(0≤x≤2015π)的极小值点的个数为( )
| A. | 1007 | B. | 1008 | C. | 2015 | D. | 2016 |
13.已知棱锥的顶点为P,P在底面上的射影为O,PO=a,现用平行于底面的平面去截这个棱锥,截面交PO于M,并使截得的两部分侧面积相等,设OM=b,则a,b的关系是( )
| A. | b=($\sqrt{2}$-1)a | B. | b=($\sqrt{2}$+1)a | C. | b=$\frac{2-\sqrt{2}}{2}$a | D. | b=$\frac{2+\sqrt{2}}{2}$a |
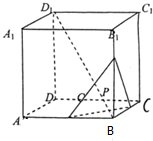 如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记平面α截正方体得到的截面多边形(含三角形)的周长为y=f(x),设BP=x,x∈(0,3),关于函数y=f(x):
如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记平面α截正方体得到的截面多边形(含三角形)的周长为y=f(x),设BP=x,x∈(0,3),关于函数y=f(x):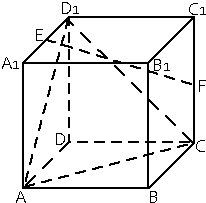 如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.
如图在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为A1D1和CC1的中点.