题目内容
18．椭圆$\frac{x^2}{25}+{y^2}$=1上一点P到焦点F1的距离等于6，则点P到另一个焦点F2的距离为（ ）| A． | 10 | B． | 8 | C． | 4 | D． | 3 |
分析 直接由椭圆的定义结合已知求解．
解答 解：由椭圆$\frac{x^2}{25}+{y^2}$=1，得a2=25，∴a=5，
又|PF1|=6，|PF1|+|PF2|=2a=10，
∴|PF2|=10-6=4．
故选：C．
点评 本题考查椭圆的简单性质，考查了椭圆定义的应用，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
6．设函数f（x）的导函数为f′（x），且f′（x）＜f（x）对于x∈R恒成立，则（ ）
| A． | e2f（-2）＞f（0），f（2）＞e2f（0） | B． | e2f（-2）＜f（0），f（2）＜e2f（0） | ||
| C． | e2f（-2）＞f（0），f（2）＜e2f（0） | D． | e2f（-2）＜f（0），f（2）＞e2f（0） |
13．已知棱锥的顶点为P，P在底面上的射影为O，PO=a，现用平行于底面的平面去截这个棱锥，截面交PO于M，并使截得的两部分侧面积相等，设OM=b，则a，b的关系是（ ）
| A． | b=（$\sqrt{2}$-1）a | B． | b=（$\sqrt{2}$+1）a | C． | b=$\frac{2-\sqrt{2}}{2}$a | D． | b=$\frac{2+\sqrt{2}}{2}$a |
10．过点A（4，$\frac{3π}{2}$）引圆ρ=4sinθ的一条切线，则切线长为（ ）
| A． | 3$\sqrt{3}$ | B． | 6$\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | 4$\sqrt{2}$ |
7．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别F1（-c，0），F2（c，0），若椭圆上存在点P，使得csin∠PF1F2=asin∠PF2F1≠0，则离心率e的取值范围是（ ）
| A． | $（0，\frac{{\sqrt{2}}}{2}）$ | B． | $（\sqrt{2}-1，1）$ | C． | $[\sqrt{2}-1，1）$ | D． | $（0，\sqrt{2}-1]$ |
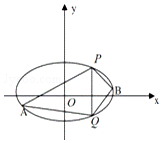已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{2}$，椭圆C的一个短轴端点与抛物线x2=4y的焦点重合．