题目内容
16.已知点P在抛物线y2=4x上,则点P到直线l1:4x-3y+11=0的距离和到l2:x=-1的距离之和的最小值为( )| A. | $\frac{37}{16}$ | B. | 3 | C. | 2 | D. | $\frac{11}{5}$ |
分析 如图所示,过点P分别作PM⊥l1,PN⊥l2,垂足分别为M,N.设抛物线的焦点为F,由抛物线的定义可得|PN|=|PF|,求|PM|+|PN|转化为求|PM|+|PF|,当三点M,P,F共线时,|PM|+|PF|取得最小值.利用点到直线的距离公式即可得出.
解答  解:如图所示,
解:如图所示,
过点P分别作PM⊥l1,PN⊥l2,垂足分别为M,N.
设抛物线的焦点为F(1,0),由抛物线的定义可得|PN|=|PF|,
∴|PM|+|PN|=|PM|+|PF|,当三点M,P,F共线时,
|PM|+|PF|取得最小值.
其最小值为点F到直线l1的距离,∴|FM|=$\frac{|4-0+11|}{\sqrt{16+9}}$=3.
故选B.
点评 本题考查了抛物线的定义及其性质、三点共线、点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
4.设函数f(x)=ex-e-x-2x,下列结论正确的是( )
| A. | f(2x)min=f(0) | B. | f(2x)max=f(0) | ||
| C. | f(2x)在(-∞,+∞)上递减,无极值 | D. | f(2x)在(-∞,+∞)上递增,无极值 |
5.在四面体P-ABC的四个面中,是直角三角形的面至多有( )个.
| A. | 0个 | B. | 1个 | C. | 3个 | D. | 4个 |
6.设函数f(x)的导函数为f′(x),且f′(x)<f(x)对于x∈R恒成立,则( )
| A. | e2f(-2)>f(0),f(2)>e2f(0) | B. | e2f(-2)<f(0),f(2)<e2f(0) | ||
| C. | e2f(-2)>f(0),f(2)<e2f(0) | D. | e2f(-2)<f(0),f(2)>e2f(0) |
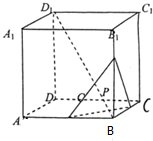 如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记平面α截正方体得到的截面多边形(含三角形)的周长为y=f(x),设BP=x,x∈(0,3),关于函数y=f(x):
如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记平面α截正方体得到的截面多边形(含三角形)的周长为y=f(x),设BP=x,x∈(0,3),关于函数y=f(x):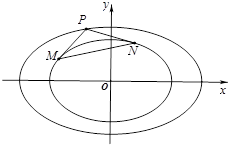 已知椭圆${C_1}:\frac{x^2}{2}+{y^2}=1$
已知椭圆${C_1}:\frac{x^2}{2}+{y^2}=1$