题目内容
19.已知函数$f(x)=sinx-\frac{1}{2}x$,x∈[0,π].那么下列命题中所有真命题的序号是①④.①f(x)的最大值是$f(\frac{π}{3})$
②f(x)的最小值是$f(\frac{π}{3})$
③f(x)在$[0,\frac{π}{3}]$上是减函数
④f(x)在$[\frac{π}{3},π]$上是减函数.
分析 先求导,再研究出它的单调性确定出最值,再由这些性质对四个命题进行比较验证,选出正确命题
解答 解:∵f(x)=sinx-$\frac{1}{2}$x,x∈[0,π],
∴f′(x)=cosx-$\frac{1}{2}$,
令f′(x)=0,解得x=$\frac{π}{3}$,
当f′(x)>0时,解得0≤x≤$\frac{π}{3}$,函数单调递增,
当f′(x)<0时,解得$\frac{π}{3}$≤x≤π,函数单调递减,
∴当x=$\frac{π}{3}$时,函数取的最大值,即f(x)的最大值是$f(\frac{π}{3})$
∵f(0)=sin0-0=0,f(π)=sinπ-$\frac{1}{2}$π=-$\frac{1}{2}$π,
∴函数的最小值为f(π)=-$\frac{1}{2}$π,
故所有真命题的序号是①④,
故答案为;①④.
点评 本题考查命题的真假的判断与应用,解题的关键是掌握住用导数判断函数的单调性及求最值,由这些结论对四个命题的正确性进行验证得出正确选项.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
9.袋中装有10个红球、5个黑球.每次随机抽取1个球后,若取得黑球则另换1个红球放回袋中,直到取到红球为止.若抽取的次数为ξ,则表示“放回5个红球”事件的是( )
| A. | ξ=4 | B. | ξ=5 | C. | ξ=6 | D. | ξ≤5 |
14.设函数f(x)=ex(sinx-cosx)(0≤x≤2015π)的极小值点的个数为( )
| A. | 1007 | B. | 1008 | C. | 2015 | D. | 2016 |
4.设函数f(x)=ex-e-x-2x,下列结论正确的是( )
| A. | f(2x)min=f(0) | B. | f(2x)max=f(0) | ||
| C. | f(2x)在(-∞,+∞)上递减,无极值 | D. | f(2x)在(-∞,+∞)上递增,无极值 |
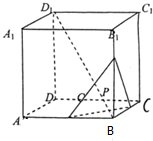 如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记平面α截正方体得到的截面多边形(含三角形)的周长为y=f(x),设BP=x,x∈(0,3),关于函数y=f(x):
如图,正方体ABCD-A1B1C1D1的棱长为$\sqrt{3}$,动点P在对角线BD1上,过点P作垂直于BD1的平面α,记平面α截正方体得到的截面多边形(含三角形)的周长为y=f(x),设BP=x,x∈(0,3),关于函数y=f(x):