题目内容
若x-4
=2
,则x的取值范围为 .
| y |
| x-y |
考点:根式与分数指数幂的互化及其化简运算
专题:函数的性质及应用
分析:要使x-4
=2
有意义,则
,可得x2≥16y≥0.对于x-4
=2
,两边平方可得:20(
)2-8x
+x2-4x=0,
此方程有非负数解,可得△≥0,
≥0,
≥0,解出即可.
| y |
| x-y |
|
| y |
| x-y |
| y |
| y |
此方程有非负数解,可得△≥0,
| x2-4x |
| 20 |
| 8x |
| 20 |
解答:
解:要使x-4
=2
有意义,则
,
∴x2≥16y≥0.
∵x-4
=2
,
两边平方可得:20(
)2-8x
+x2-4x=0,
∵此方程有非负数解,
∴△=64x2-80(x2-4x)≥0,
≥0,
≥0,
解得4≤x≤20,或x=0.
∴x的取值范围为[4,20]∪{0}.
故答案为:[4,20]∪{0}.
| y |
| x-y |
|
∴x2≥16y≥0.
∵x-4
| y |
| x-y |
两边平方可得:20(
| y |
| y |
∵此方程有非负数解,
∴△=64x2-80(x2-4x)≥0,
| x2-4x |
| 20 |
| 8x |
| 20 |
解得4≤x≤20,或x=0.
∴x的取值范围为[4,20]∪{0}.
故答案为:[4,20]∪{0}.
点评:本题考查了一元二次有实数解与判别式的关系、根与系数的关系、根式函数的定义域,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
若2sina=3cosa,则
的值为( )
| 4sina+cosa |
| 5sina-2cosa |
A、
| ||||
| B、2 | ||||
C、-
| ||||
D、
|
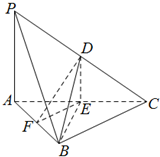 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.