题目内容
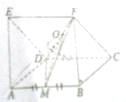 如图,在直三棱柱ADE-BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运动向量方法证明:
如图,在直三棱柱ADE-BCF中,面ABFE和面ABCD都是正方形且互相垂直,M为AB的中点,O为DF的中点,运动向量方法证明:(1)OM∥平面BCF;
(2)平面MDF⊥平面EFCD.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离,空间向量及应用
分析:(1)以A为原点建立如图所示的空间直角坐标系,设正方形边长为1,则先求A,B,C,D,F,M,O等点的坐标,再求
,
的坐标,可证
⊥
,从而可证OM∥平面BCF.
(2)设平面MDF与平面EFCD的一个法向量分别是n1=(x1,y1,z1),n2=(x2,y2,z2).由n1•
=n1•
=0,解得n1,n2的值,则可得n1•n2=0,从而可证平面MDF⊥平面EFCD.
| OM |
| BA |
| OM |
| BA |
(2)设平面MDF与平面EFCD的一个法向量分别是n1=(x1,y1,z1),n2=(x2,y2,z2).由n1•
| DF |
| DM |
解答:

证明:(1)由题意,AB,AD,AE两两垂直,以A为原点建立如图所示的空间直角坐标系.
设正方形边长为1,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),F(1,0,1),M(
,0,0),O(
,
,
)
=(0,-
,-
),
=(-1,0,0)
∴
•
=0
∴
⊥
.
∵三棱柱ADE-BCF是直三棱柱,
∴AB⊥平面BCF,∴
是平面BCF的一个法向量,且OM?平面BCF,
∴OM∥平面BCF.
(2)设平面MDF与平面EFCD的一个法向量分别是n1=(x1,y1,z1),n2=(x2,y2,z2).
∵
=(1,-1,1),
=(
,-1,0),
=(1,0,0),
由n1•
=n1•
=0,得
解得
令x1=1,则n1=(1,
,-
).
同理可得n2=(0,1,1),
∵n1•n2=0
∴平面MDF⊥平面EFCD.

证明:(1)由题意,AB,AD,AE两两垂直,以A为原点建立如图所示的空间直角坐标系.
设正方形边长为1,则A(0,0,0),B(1,0,0),C(1,1,0),D(0,1,0),F(1,0,1),M(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| OM |
| 1 |
| 2 |
| 1 |
| 2 |
| BA |
∴
| OM |
| BA |
∴
| OM |
| BA |
∵三棱柱ADE-BCF是直三棱柱,
∴AB⊥平面BCF,∴
| BA |
∴OM∥平面BCF.
(2)设平面MDF与平面EFCD的一个法向量分别是n1=(x1,y1,z1),n2=(x2,y2,z2).
∵
| DF |
| DM |
| 1 |
| 2 |
| DC |
由n1•
| DF |
| DM |
|
解得
|
令x1=1,则n1=(1,
| 1 |
| 2 |
| 1 |
| 2 |
同理可得n2=(0,1,1),
∵n1•n2=0
∴平面MDF⊥平面EFCD.
点评:本题的证明,可以用几何法,也可以用向量法,用向量法的关键在于构造向量,再用共线向量定理或共面向量定理及两向量垂直的判定定理.若能建立空间直角坐标系,其证法较为灵活方便,本题属于中档题.

练习册系列答案
相关题目
若2sina=3cosa,则
的值为( )
| 4sina+cosa |
| 5sina-2cosa |
A、
| ||||
| B、2 | ||||
C、-
| ||||
D、
|
直线
x+y-2=0与圆x2+y2=4交于A,B两点,则|AB|=( )
| 3 |
| A、1 | ||
B、2
| ||
C、2
| ||
| D、2 |
先后抛掷两颗骰子,则所得点数之和为7的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
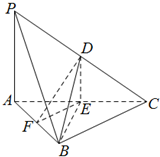 如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.
如图,在三棱锥P-ABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=AB=6,BC=8,DF=5.