题目内容
16.设函数f(x)=|2x-1|,函数g(x)=f(f(x))-loga(x+1),(a>0,a≠1)在[0,1]上有3个不同的零点,则实数a的取值范围为( )| A. | (1,$\frac{3}{2}$) | B. | (1,2) | C. | ($\frac{3}{2}$,2) | D. | (2,+∞) |
分析 作出两个函数的图象,结合对数函数的单调性,利用数形结合即可得到结论.
解答 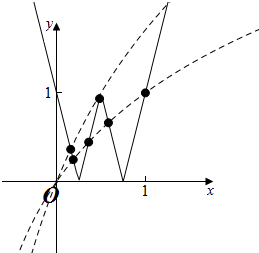 解:∵f(x)=|2x-1|=$\left\{\begin{array}{l}{2x-1,x≥\frac{1}{2}}\\{-2x+1,x<\frac{1}{2}}\end{array}\right.$,
解:∵f(x)=|2x-1|=$\left\{\begin{array}{l}{2x-1,x≥\frac{1}{2}}\\{-2x+1,x<\frac{1}{2}}\end{array}\right.$,
∴f(f(x))=|2|2x-1|-1|=$\left\{\begin{array}{l}{4x-3,x>\frac{3}{4}}\\{-4x+3,\frac{1}{2}<x≤\frac{3}{4}}\\{4x-1,\frac{1}{4}<x≤\frac{1}{2}}\\{-4x+1,x≤\frac{1}{4}}\end{array}\right.$
分别画出y=f(f(x))与y=loga(x+1)的图象,
∵y=loga(x+1)的图象是由y=logax的图象向左平移一个单位得到的,且过点(0,0),
当x=1时,y=f(f(1))=1,
此时loga(1+1)=1,解得a=2,有4个交点,
当x=$\frac{1}{2}$时,y=f(f($\frac{1}{2}$))=1,
此时loga($\frac{1}{2}$+1)=1,解得a=$\frac{3}{2}$,有2个交点,
综上所述a的取值范围为($\frac{3}{2}$,2)
故选:C.
点评 本题主要考查函数交点个数的判断以及对数函数的单调性,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
6.在直角坐标系xOy平面上,平行直线x=m(m=0,1,2,3,4),与平行直线y=n(n=0,1,2,3,4)组成的图形中,矩形共有( )
| A. | 25个 | B. | 100个 | C. | 36个 | D. | 200个 |
4.Rt△ABC顶点A(0,0),B(0,4),C(-2,0),则△ABC内角∠A的平分线方程是( )
| A. | y=-x | B. | y=-$\frac{1}{2}$x(-$\frac{6}{5}$≤x≤0) | C. | y=-x(-$\frac{4}{5}$≤x≤0) | D. | y=-$\frac{1}{2}$x |
16.已知f(x)为定义在R上的可导函数,且f(x)>f′(x)对于x∈R恒成立.若e为自然对数的底数,则下列关系一定成立的是( )
| A. | e2015f(2015)>e2016f(2016) | B. | e2015f(2015)<e2016f(2016) | ||
| C. | e2015f(2016)>e2016f(2015) | D. | e2015f(2016)<e2016f(2015) |
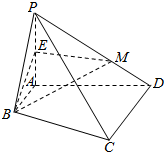 如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.
如图,在四棱锥P-ABCD中,平面PAB⊥平面ABCD,AB∥CD,AB⊥AD,CD=2AB,E为PA的中点,M在PD上.