题目内容
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
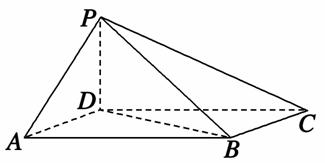
(1)证明:PA⊥BD;
(2)设PD=AD,求二面角A-PB-C的余弦值.
(1)因为∠DAB=60°,AB=2AD,
由余弦定理得BD=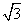 AD.
AD.
从而BD2+AD2=AB2,故BD⊥AD.
又PD⊥底面ABCD,可得BD⊥PD.
所以BD⊥平面PAD,故PA⊥BD.
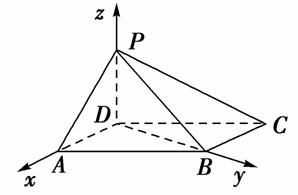
(2)如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴,建立空间直角坐标系D-xyz,则A(1,0,0),B(0,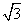 ,0),C(-1,
,0),C(-1,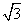 ,0),P(0,0,1).
,0),P(0,0,1).
 可取m=(0,-1,-
可取m=(0,-1,-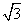 ).cos〈m,n〉=
).cos〈m,n〉=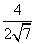 =-
=-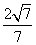 .
.
故二面角A-PB-C的余弦值为-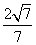 .
.

练习册系列答案
相关题目
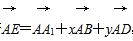 ,则x,y的值分别为( )
,则x,y的值分别为( )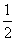

 B.-
B.-
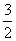 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
 ,则y=( )
,则y=( ) 与圆
与圆 的位置关系是( )
的位置关系是( ) 的值有关
的值有关