题目内容
如图,四棱锥P-ABCD中,PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1,PA=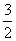 ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
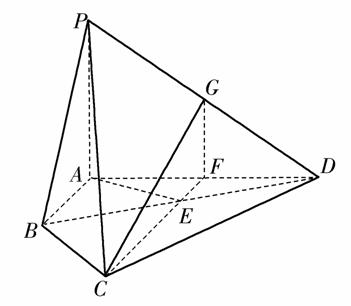
(1)求证:AD⊥平面CFG;
(2)求平面BCP与平面DCP的夹角的余弦值.
[解析] (1)△ABD中,因为E是BD中点,
所以EA=EB=ED=AB=1,
故∠BAD= ,∠ABE=∠AEB=
,∠ABE=∠AEB= ,
,
因为△DAB≌△DCB,所以△EAB≌△ECB,
从而有∠FED=∠BEC=∠AEB= ,
,
所以∠FED=∠FEA,
故EF⊥AD,AF=FD,又因为PG=GD,所以FG∥PA.
又PA⊥平面ABCD.
所以GF⊥AD.故AD⊥平面CFG.
(2)以点A为坐标原点建立如图所示的坐标系,则

A(0,0,0),B(1,0,0),C(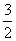 ,
,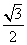 ,0),D(0,
,0),D(0,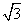 ,0),P(0,0,
,0),P(0,0,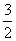 ),
),
故
 即n2=(1,
即n2=(1,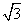 ,2)从而平面BCP与平面DCP的夹角的余弦值为
,2)从而平面BCP与平面DCP的夹角的余弦值为


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 |的取值范围是____________.
|的取值范围是____________. 则错误命题的序号是________(填出所有错误命题的序号).
则错误命题的序号是________(填出所有错误命题的序号). B.
B.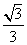
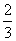 D.
D.

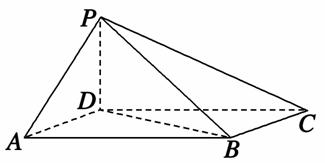
 的定义域为
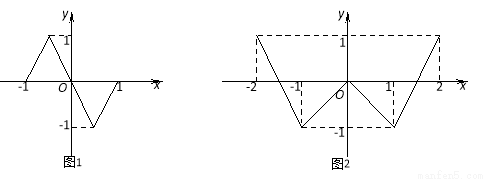
的定义域为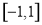 ,图象如图1所示;函数
,图象如图1所示;函数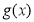 的定义域为
的定义域为 ,图象如图2所示,方程
,图象如图2所示,方程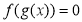 有
有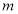 个实数根,方程
个实数根,方程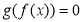 有
有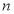 个实数根,则
个实数根,则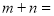 ( )
( )