题目内容
用“更相减损术”求98和63的最大公约数，要做减法的次数是（ ）
| A、3次 | B、4次 | C、5次 | D、6次 |
考点：用辗转相除计算最大公约数
专题：计算题,算法和程序框图
分析：我们根据“以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数．继续这个操作，直到所得的减数和差相等为止．”的原则，易求出98和63的最大公约数．统计减法次数可得答案．
解答：
解：用“更相减损术”求98和63的最大公约数，
98-63=35，
63-35=28，
35-28=7，
28-7=21，
21-7=14，
14-7=7，
共需要6次减法运算，
故选：D
98-63=35，
63-35=28，
35-28=7，
28-7=21，
21-7=14，
14-7=7，
共需要6次减法运算，
故选：D
点评：本题考查的知识点是最大公因数和更相减损术，更相减损术的方法和步骤是：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数．继续这个操作，直到所得的减数和差相等为止．
练习册系列答案
相关题目
边长为1的正六边形ABCDEF中，点P是正六边形内的一点（含边界），则
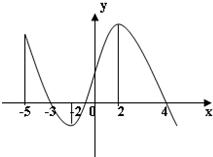如图所示是f′（x）的图象，则正确的判断个数是（ ）（1）f（x）在（-5，-3）上是减函数；
（2）x=4是极大值点；
（3）x=2是极值点；
（4）f（x）在（-2，2）上先减后增．
| A、0 | B、1 | C、2 | D、3 |
已知等差数列{an}中a2+a3+a7+a8=20，则该数列前9项和S9等于（ ）
| A、18 | B、27 | C、36 | D、45 |
数列
，-
，
，-
…的一个通项公式是（ ）
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 8 |
| 7 |
| 16 |
A、an=（-1）n•
| ||
B、an=（-1）n+1•
| ||
C、an=（-1）n•
| ||
D、an=（-1）n+1•
|
一物体的运动方程为s=t2-2t+5，其中s的单位是米，t的单位是秒，那么物体在4秒末的瞬时速度是（ ）
| A、8米/秒 | B、7米/秒 |
| C、6米/秒 | D、5米/秒 |
若a＞b，则下列不等式成立的是（ ）
A、
| ||||||
| B、a＞|b| | ||||||
C、
| ||||||
| D、lna＞lnb |