题目内容
设有二元关系f(x,y)=(x-y)2+a(x-y)-1,已知曲线г:f(x,y)=0
(1)若a=2时,正方形 ABCD的四个顶点均在曲线上г,求正方形ABCD的面积;
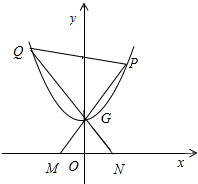
(2)设曲线г与x轴的交点是M、N,抛物线г′:y=
x2+1与 y 轴的交点是G,直线MG与曲线г′交于点P,直线NG 与曲线г′交于Q,求证:直线PQ过定点,并求出该定点的坐标.
(3)设曲线г与x轴的交点是M(u,0),N(v,0),可知动点R(u,v)在某确定的曲线∧上运动,曲线∧与上述曲线г在a≠0时共有四个交点:A(x1,x2),B(x3,x4),C(x5,x6),D(x7,x8),集合X={x1,x2,…,x8}的所有非空子集设为Yi(i=1,2,…,255),将Yi中的所有元素相加(若i Y 中只有一个元素,则其是其自身)得到255 个数y1,y2,…,y255求所有的正整数n 的值,使得y1n+y2n+…+y255n 是与变数a及变数xi(i=1,2,…8)均无关的常数.
(1)若a=2时,正方形 ABCD的四个顶点均在曲线上г,求正方形ABCD的面积;
(2)设曲线г与x轴的交点是M、N,抛物线г′:y=
| 1 |
| 2 |
(3)设曲线г与x轴的交点是M(u,0),N(v,0),可知动点R(u,v)在某确定的曲线∧上运动,曲线∧与上述曲线г在a≠0时共有四个交点:A(x1,x2),B(x3,x4),C(x5,x6),D(x7,x8),集合X={x1,x2,…,x8}的所有非空子集设为Yi(i=1,2,…,255),将Yi中的所有元素相加(若i Y 中只有一个元素,则其是其自身)得到255 个数y1,y2,…,y255求所有的正整数n 的值,使得y1n+y2n+…+y255n 是与变数a及变数xi(i=1,2,…8)均无关的常数.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)令f(x,y)=(x-y)2+2(x-y)-1=0,解得x-y=-1±
,由于f(x,y)表示两条平行线,之间的距离是2,为一个正方形,即可得出面积S.
(2):在曲线C中,令y=0,则x2+ax-1=0,设M(m,0),N(n,0),则mn=-1,G(0,1),
则直线MG:y=-
x+1,NG:y=-
x+1.分别与抛物线方程联立可得P(-
,
),Q(-
,
).直线PQ的方程为:y-
-1=(m+n)(x+
),令x=0,可得y=3,因此直线PQ过定点(0,3).
(3)令y=0,则x2+ax-1=0,则mn=-1,即点R(u,v)在曲线xy=-1上,又曲线C:f(x,y)=0.恒表示平行线x-y=
,A(x1,x2),B(x3,x4)关于直线y=-x对称,即x1+x2+x3+x4=0,同理可得x5+x6+x7+x8=0,则x1+x2+…+x8=0,集合X={x1,x2,…,x8}的所有非空子集设为Yi=1,2,…,255),取Y1={x1,x2,…,x8},则y1=x1+x2+…+x8=0,即n∈N*,
=0,对X的其它子集,把它们配成集合“对”(Yp,Yq),Yp∪Yq=X,Yp∩Yq=∅,这样的集合“对”共有127对,且对每一个集合“对”都满足yp+yq=0.可以利用扇形归纳法证明:对于Yp的元素和yp与Yq的元素和yq,当n为奇数时,
+
=0.即可得出.
| 2 |
(2):在曲线C中,令y=0,则x2+ax-1=0,设M(m,0),N(n,0),则mn=-1,G(0,1),
则直线MG:y=-
| 1 |
| m |
| 1 |
| n |
| 2 |
| m |
| 2+m2 |
| m |
| 2 |
| n |
| 2+n2 |
| n |
| 2 |
| n2 |
| 2 |
| n |
(3)令y=0,则x2+ax-1=0,则mn=-1,即点R(u,v)在曲线xy=-1上,又曲线C:f(x,y)=0.恒表示平行线x-y=
-a±
| ||
| 2 |
| y | n 1 |
| y | n p |
| y | n q |
解答:
 解:(1)令f(x,y)=(x-y)2+2(x-y)-1=0,解得x-y=-1±
解:(1)令f(x,y)=(x-y)2+2(x-y)-1=0,解得x-y=-1±
,
∴f(x,y)=0表示两条平行线,之间的距离是2,此为一个正方形的一个边长,其面积S=4.
(2)证明:在曲线C中,令y=0,则x2+ax-1=0,
设M(m,0),N(n,0),则mn=-1,G(0,1),
则直线MG:y=-
x+1,NG:y=-
x+1.
联立
,解得P(-
,
),
同理可得Q(-
,
).
∴直线PQ的方程为:y-
-1=(m+n)(x+
)
令x=0,则y=
+1+(m+n)
=
+1+(-
+n)
=3,
因此直线PQ过定点(0,3).
(3)令y=0,则x2+ax-1=0,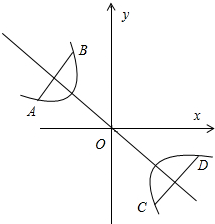
则mn=-1,即点R(u,v)在曲线xy=-1上,
又曲线C:f(x,y)=(x-y)2+a(x-y)-1=0.
恒表示平行线x-y=
,如图所示,
A(x1,x2),B(x3,x4)关于直线y=-x对称,则
=-
,即x1+x2+x3+x4=0,
同理可得x5+x6+x7+x8=0,则x1+x2+…+x8=0,
集合X={x1,x2,…,x8}的所有非空子集设为Yi,
取Y1={x1,x2,…,x8},则y1=x1+x2+…+x8=0,即n∈N*,
=0,
对X的其它子集,把它们配成集合“对”(Yp,Yq),Yp∪Yq=X,Yp∩Yq=∅,
这样的集合“对”共有127对,且对每一个集合“对”都满足yp+yq=0.
以下证明:对于Yp的元素和yp与Yq的元素和yq,当n为奇数时,
+
=0.
先证明:n为奇数时,x+y能够整除xn+yn,用数学归纳法证明.
1°当n=1时,成立;
2°假设当n=k(奇数)时,x+y能够整除xk+yk,
则当n=k+2时,xk+2+yk+2=xk+2-xky2+xky2+yk+2=xk(x2-y2)+y2(xk+yk),
因此上式可被x+y整除.
由1°,2°可知:n为奇数时,x+y能够整除xn+yn.
又∵当n为奇数时,
+
=(yp+yq)M,其中M是关于yp,yq的整式,
∵Yp∪Yq=X,Yp∩Yq=∅,
∴每一个集合“对”(Yp,Yq)都满足yp+yq=0.则一定有
+
=(x+y)M=0,M∈N*,
于是可得y1n+y2n+…+y255n=0是常数.
 解:(1)令f(x,y)=(x-y)2+2(x-y)-1=0,解得x-y=-1±
解:(1)令f(x,y)=(x-y)2+2(x-y)-1=0,解得x-y=-1±| 2 |
∴f(x,y)=0表示两条平行线,之间的距离是2,此为一个正方形的一个边长,其面积S=4.
(2)证明:在曲线C中,令y=0,则x2+ax-1=0,
设M(m,0),N(n,0),则mn=-1,G(0,1),
则直线MG:y=-
| 1 |
| m |
| 1 |
| n |
联立
|
| 2 |
| m |
| 2+m2 |
| m2 |
同理可得Q(-
| 2 |
| n |
| 2+n2 |
| n2 |
∴直线PQ的方程为:y-
| 2 |
| n2 |
| 2 |
| n |
令x=0,则y=
| 2 |
| n2 |
| 2 |
| n |
| 2 |
| n2 |
| 1 |
| n |
| 2 |
| n |
因此直线PQ过定点(0,3).
(3)令y=0,则x2+ax-1=0,

则mn=-1,即点R(u,v)在曲线xy=-1上,
又曲线C:f(x,y)=(x-y)2+a(x-y)-1=0.
恒表示平行线x-y=
-a±
| ||
| 2 |
A(x1,x2),B(x3,x4)关于直线y=-x对称,则
| x1+x3 |
| 2 |
| x2+x4 |
| 2 |
同理可得x5+x6+x7+x8=0,则x1+x2+…+x8=0,
集合X={x1,x2,…,x8}的所有非空子集设为Yi,
取Y1={x1,x2,…,x8},则y1=x1+x2+…+x8=0,即n∈N*,
| y | n 1 |
对X的其它子集,把它们配成集合“对”(Yp,Yq),Yp∪Yq=X,Yp∩Yq=∅,
这样的集合“对”共有127对,且对每一个集合“对”都满足yp+yq=0.
以下证明:对于Yp的元素和yp与Yq的元素和yq,当n为奇数时,
| y | n p |
| y | n q |
先证明:n为奇数时,x+y能够整除xn+yn,用数学归纳法证明.
1°当n=1时,成立;
2°假设当n=k(奇数)时,x+y能够整除xk+yk,
则当n=k+2时,xk+2+yk+2=xk+2-xky2+xky2+yk+2=xk(x2-y2)+y2(xk+yk),
因此上式可被x+y整除.
由1°,2°可知:n为奇数时,x+y能够整除xn+yn.
又∵当n为奇数时,
| y | n p |
| y | n q |
∵Yp∪Yq=X,Yp∩Yq=∅,
∴每一个集合“对”(Yp,Yq)都满足yp+yq=0.则一定有
| y | n p |
| y | n q |
于是可得y1n+y2n+…+y255n=0是常数.
点评:本题考查了平行直线系、直线的交点、一元二次方程的根与系数的关系、集合的性质、中点坐标公式、对称性、扇形归纳法,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知函数f(x)=lnx+
x2-2x+2在[et,+∞)(t∈Z)上有零点,则t的最大值为( )
| 3 |
| 8 |
| A、0 | B、-1 | C、-2 | D、2 |
 已知三棱柱ABC-A1B1C1的侧棱与底面ABC垂直,且AA1=4,AC=BC=2,∠ACB=90°.
已知三棱柱ABC-A1B1C1的侧棱与底面ABC垂直,且AA1=4,AC=BC=2,∠ACB=90°. 如图,AB=5cm,BC⊥AB,BD⊥AB,在BC,BD所在的平面α内任取一点E,BE=7cm.
如图,AB=5cm,BC⊥AB,BD⊥AB,在BC,BD所在的平面α内任取一点E,BE=7cm. 如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点
如图,在棱长为2的正方体AC′中,E,F为BC和AA′的中点