题目内容

函数f（x）=（1-x）ex的单调递减区间是
 
．
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：求导，令导数小于0，得x的取值区间，即为f（x）的单调减区间．
解答： 解：f′（x）=[（1-x）•ex]′=-ex+（1-x）•ex=-xex，
令f′（x）＜0得x＞0，
∴函数f（x）的单调递减区间为（0，+∞）．
故答案为（0，+∞）．
点评：考查利用导数求函数的单调区间，利用函数单调性和导数之间的关系是解决本题的关键．
练习册系列答案
相关题目
设全集U=Z，集合M={0，2，4}，N={-1，0，3}，则图中阴影部分表示的集合是（　　）
A、{-1，3}B、{1，5}
C、{2，4}D、{0}
已知函数f（x）=ax-bx2
（1）当b＞0时，若对任意x∈R都有f（x）≤1求证a≤2
b
．
（2）当b＞1时，求证；对任意x∈[0，1]，|f（x）|≤1的充要条件是b-1≤a≤2
b
．
已知点（-3，-1）和（4，-6）在直线3x-2y-a=0的两侧，则a的取值范围是
 
．
若
cos(2α+π)
sin(α-
π
4
)
=
2
2
，则sinα+cosα的值为（　　）
A、-
7
2
B、-
1
2
C、
1
2
D、
7
2
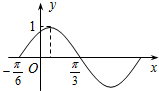函数f（x）=Asin（ωx+φ）(A＞0，ω＞0，|φ|＜
π
2
)的部分图象如图所示，若x1，x2∈(-
π
6
，
π
3
)，且f（x1）=f（x2）（x1≠x2），则f（x1+x2）=（　　）
A、1
B、
1
2
C、
2
2
D、
3
2
已知函数f（x）是周期为2的偶函数，且在x∈[0，1]时，f（x）=x，若直线kx-y+k=0（k＞0）与函数f（x）的图象有且仅有三个公共点，则k的取值范围是（　　）
A、(0，
1
2
)
B、(0，
1
2
]
C、(
1
4
，
1
2
)
D、[
1
4
，
1
2
)
已知函数f（x）=3sin（ωx+φ）（ω＞0），若f(
π
3
)=3，f(
π
12
)=0，则ω的最小值为（　　）
A、2B、4C、6D、8
函数f（x）=
2x+1
+
1
x-3
的定义域为（　　）
A、（-∞，3）∪（3，+∞）
B、[-
1
2
，3）∪（3，+∞）
C、（-
1
2
，3）∪（3，+∞）
D、[-
1
2
，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网