��Ŀ����
7��������•ţ�٣�1643��1��4��-1727��3��31�գ�Ӣ���ʼ�ѧ��᳤��Ӣ����������ѧ�ң�ͬʱ����ѧ��Ҳ������ܳ����ף�ţ���á������ߡ��ķ�������f��x�����ʱ����һ������{xn}������${x_{n+1}}={x_n}-\frac{{f��{x_n}��}}{{f'��{x_n}��}}$�����ǰѸ����г�Ϊţ�����У��������f��x��=ax2+bx+c��a��0�����������1��2������{xn}Ϊţ�����У���${a_n}=ln\frac{{{x_n}-2}}{{{x_n}-1}}$����֪a1=2��xn��2����{an}��ͨ�ʽan=2n������ ����֪�õ�a��b��c�Ĺ�ϵ���ɵ�f��x��=ax2-3ax+2a�������${x_{n+1}}={x_n}-\frac{{f��{x_n}��}}{{f'��{x_n}��}}$�������ɵ�$\frac{{x}_{n+1}-2}{{x}_{n+1}-1}=��\frac{{x}_{n}-2}{{x}_{n}-1}��^{2}$������ȡ�������ɵ�$ln\frac{{x}_{n}-2}{{x}_{n}-1}$����2Ϊ���ȵĵȱ����У����ɵȱ����е�ͨ�ʽ�𰸣�
��� �⣺�ߺ���f��x��=ax2+bx+c��a��0�����������1��2��
��$\left\{\begin{array}{l}{a+b+c=0}\\{4a+2b+c=0}\end{array}\right.$����ã�$\left\{\begin{array}{l}{c=2a}\\{b=-3a}\end{array}\right.$��
��f��x��=ax2-3ax+2a��
��f�䣨x��=2ax-3a��
��${x}_{n+1}={x}_{n}-\frac{a{{x}_{n}}^{2}-3a{x}_{n}+2a}{2a{x}_{n}-3a}$=${x}_{n}-\frac{{{x}_{n}}^{2}-3{x}_{n}+2}{2{x}_{n}-3}$=$\frac{{{x}_{n}}^{2}-2}{2{x}_{n}-3}$��
��$\frac{{x}_{n+1}-2}{{x}_{n+1}-1}=��\frac{{x}_{n}-2}{{x}_{n}-1}��^{2}$��
��$ln\frac{{x}_{n}-2}{{x}_{n}-1}$����2Ϊ���ȵĵȱ����У�
��${a_n}=ln\frac{{{x_n}-2}}{{{x_n}-1}}$����a1=2��
������{an}����2Ϊ�����2Ϊ���ȵĵȱ����У�
��${a}_{n}=2•{2}^{n-1}={2}^{n}$��
�ʴ�Ϊ��2n��
���� ���⿼�����е���ʽ�������˵ȱȹ�ϵ��ȷ�������е��⣮

 ���Ǽ���С����ϵ�д�
���Ǽ���С����ϵ�д� �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д�| A�� | ��С������Ϊ�е��溯�� | B�� | ��С������Ϊ$\frac{��}{2}$��ż���� | ||
| C�� | ��С������Ϊ$\frac{��}{2}$���溯�� | D�� | ��С������Ϊ�е�ż���� |
| A�� | ?x��R��x3��x | B�� | ?x��R��x3��x | C�� | ?x��R��x3��x | D�� | ?x0��R��x03��x0 |
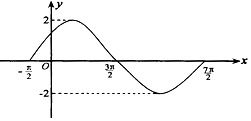 ��֪f��x��=Asin����x+�գ�������A��0���أ�0��0���գ��У���һ��������ͼ����ͼ��ʾ��
��֪f��x��=Asin����x+�գ�������A��0���أ�0��0���գ��У���һ��������ͼ����ͼ��ʾ��