题目内容
(1)根据下面的要求,求S=13+23+…+1023值.请完成执行该问题的程序框图.
(2)请运用更相减损术求459与357的最大公约数.

(2)请运用更相减损术求459与357的最大公约数.

考点:程序框图
专题:算法和程序框图
分析:(1)分析题目中的要求,发现这是一个累加型的问题,故可能用循环结构来实现,在编写算法的过程中要注意,累加的初始值为0,累加值每一次增加1,把握住以上要点不难得到正确的算法和流程图.
(2)根据辗转相除法:用较大的数字除以较小的数字,得到商和余数,然后再用上一式中的除数和得到的余数中较大的除以较小的,以此类推,当整除时,就得到要求的最大公约数.
(2)根据辗转相除法:用较大的数字除以较小的数字,得到商和余数,然后再用上一式中的除数和得到的余数中较大的除以较小的,以此类推,当整除时,就得到要求的最大公约数.
解答:
(本小题满分8分)
解:(1)

(2)因为459-357=102
357-102=255
255-102=153
153-102=51
102-51=51
所以459与357的最大公约数为51.
解:(1)

(2)因为459-357=102
357-102=255
255-102=153
153-102=51
102-51=51
所以459与357的最大公约数为51.
点评:本题考查的知识点是辗转相除法,程序算法和框图,属于基本知识的考查.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
小明参加“欧洲六国游”旅行,其中A、B、C三国游览的先后顺序一定(游A、B、C三国的顺序可以相邻也可以不相邻)则小明“欧洲六国游”旅行共有( )种不同的出游方法.
| A、120 | B、180 |
| C、240 | D、480 |
下列说法不正确的是( )
| A、若“p且q”为假,则p、q至少有一个是假命题 | ||
| B、命题“?x0∈R,x02-x0-1<0”的否定是“?x∈R,x2-x-1≥0” | ||
C、“φ=
| ||
| D、a<0时,幂函数y=xa在(0,+∞)上单调递减 |
已知函数f(x)=kx,g(x)
,若关于x的方程f(x)=g(x)在区间[
,e]内有两个实数解,则实数k的取值范围是( )
| lnx |
| x |
| 1 |
| e |
A、[
| ||||
B、(
| ||||
C、(0,
| ||||
D、(
|
直线l:
x-y-
=0,圆C:(x-3)2+y2=4,直线l与圆C交于A,B两点,则
•
等于( )
| 3 |
| 3 |
| AB |
| AC |
| A、2 | ||
| B、3 | ||
| C、4 | ||
D、2
|
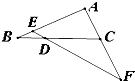 如图,在△ABC中,已知点D是BC边的三等分点且BD=
如图,在△ABC中,已知点D是BC边的三等分点且BD=