题目内容
14.函数y=x3-3x2-9x(0<x<4)有( )| A. | 极大值5,极小值-27 | B. | 极大值5,极小值-11 | ||
| C. | 极大值5,无极小值 | D. | 极小值-27,无极大值 |
分析 求导,令f′(x)=0,解方程,分析导函数符号的变化,从而可知函数的极值.
解答 解:由已知得f′(x)=3x2-6x-9
f′(x)=0⇒x1=-1,x2=3
又函数f(x)的定义域是0<x<4,则x变化时,f′(x)的变化情况如下:
当0<x<3时,f′(x)<0函数f(x)是u减函数,
当3<x<4时,f′(x)>0函数f(x)是增函数,
当x=3时,函数f(x)取得极小值为-27.
由极小值没有极大值.
故选:D.
点评 考查利用导数研究函数的极值问题,注意导数的求法,属基础题.

练习册系列答案
相关题目
4.若空间中有n(n≥5)个点,满足任意四个点都不共面,且任意两点的连线都与其它任意三点确定的平面垂直,则这样的n值( )
| A. | 不存在 | B. | 有无数个 | C. | 等于5 | D. | 最大值为8 |
6.在调查480名男人中有38名患有色盲,520名女人中有6名患有色盲,根据调查数据作出如下的列联表:
利用独立性检验的方法来判断色盲与性别有关?你所得到的结论在什么范围内有效?
注:χ2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
P(χ2≥10.828)≈0.001,P(χ2≥5.024)≈0.025,P(χ2≥6.635)≈0.01.
| 色盲 | 不色盲 | 合计 | |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 合计 | 44 | 956 | 1000 |
注:χ2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
P(χ2≥10.828)≈0.001,P(χ2≥5.024)≈0.025,P(χ2≥6.635)≈0.01.
4.有6列火车在某车站并行的6条轨道上,若快车A不能停在第1道上,货车B不能停在第6道上,则6列火车的停车方法共有( )
| A. | 480种 | B. | 720种 | C. | 504种 | D. | 600种 |
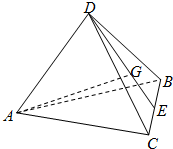 如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$.
如图,在四面体ABCD中,AB=1,AC=2,AD=3,∠DAB=∠DAC=60°,∠BAC=90°,G为△DBC的重心,则AG=$\frac{\sqrt{23}}{3}$. 图中的三个正方形块中,着色的正方形的个数依次构成一个数列{an},根据着色的规律,则a4=585,数列{an}的通项公式an=$\frac{{8}^{n}-1}{7}$.
图中的三个正方形块中,着色的正方形的个数依次构成一个数列{an},根据着色的规律,则a4=585,数列{an}的通项公式an=$\frac{{8}^{n}-1}{7}$.