题目内容
8．函数y=x3+3ax2+（a2+3a-1）x+a在x=-1时取得极值，则a=1，2．分析 求出函数的导数，利用导数为0，结合函数的极值点，求解a即可．
解答 解：函数y=x3+3ax2+（a2+3a-1）x+a，
可得y′=3x2+6ax+a2+3a-1，
函数y=x3+3ax2+（a2+3a-1）x+a在x=-1时取得极值，
y′（-1）=3-6a+a2+3a-1=0，解得a=1，a=2．
故答案为：1，2．
点评 本题考查函数的导数的应用，函数的极值点的应用，考查计算能力．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
18．一几何体的三视图如图所示，则该几何体的各个面中面积最大的面的面积为（ ）
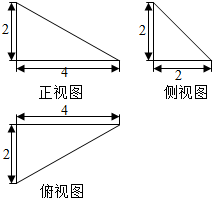
| A． | 4 | B． | 5 | C． | $\frac{9}{2}$ | D． | 6 |
19．设Sn为等差数列{an}的前n项和，若a3=3，S9-S6=27，则该数列的首项a1等于（ ）
| A． | $-\frac{6}{5}$ | B． | $-\frac{3}{5}$ | C． | $\frac{6}{5}$ | D． | $\frac{3}{5}$ |
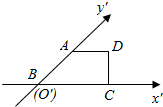有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形（如图）∠ABC=45°，AB=$\sqrt{2}$，AD=1，DC⊥BC，则这块菜地的面积为$3\sqrt{2}$．
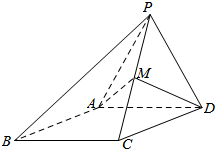如图，四棱锥P-ABCD，侧面PAD是边长为2的正三角形，且与底面ABCD垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．
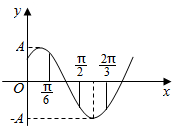函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0）的图象如图所示，若$f（{\frac{π}{2}}）=f（{\frac{2π}{3}}）=-f（{\frac{π}{6}}）$，则ω=2．