题目内容
8.已知实数x,y满足$\left\{\begin{array}{l}{2x+y≥4}\\{4x-y≤8}\\{x-y≥-1}\end{array}\right.$,则x2+y2-2x的取值范围是[-$\frac{1}{5}$,24].分析 画出可行域,通过目标函数的几何意义求解即可.
解答 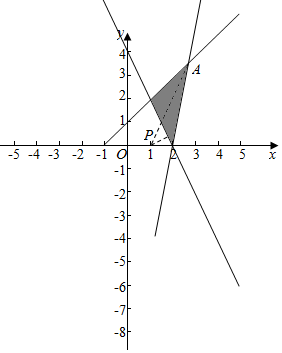 解:先根据约束条件$\left\{\begin{array}{l}{2x+y≥4}\\{4x-y≤8}\\{x-y≥-1}\end{array}\right.$,画出可行域,
解:先根据约束条件$\left\{\begin{array}{l}{2x+y≥4}\\{4x-y≤8}\\{x-y≥-1}\end{array}\right.$,画出可行域,
z=x2+y2-2x,
表示可行域内点到点P(1,0)距离的平方再减去1,
点P到直线2x+y-4=0的距离是点P到区域内的最小值,
d=$\frac{|2-4|}{\sqrt{{2}^{2}+1}}$=$\frac{2}{\sqrt{5}}$,
∴z=x2+y2-2x的最小值为-$\frac{1}{5}$;
由$\left\{\begin{array}{l}{4x-y=8}\\{x-y=-1}\end{array}\right.$,可得A(3,4)
点P到点A的距离是点P到区域内的最大值,此时d=5
∴z=x2+y2-2x的最大值为 24;
故答案为:[-$\frac{1}{5}$,24].
点评 本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础,纵观目标函数包括线性的与非线性,非线性问题的介入是线性规划问题的拓展与延伸,使得规划问题得以深化.

练习册系列答案
相关题目
19.已知O在△ABC内,∠AOB=∠BOC=∠COA=120°,且AB⊥AC,AB=3,BC=5,则$\overrightarrow{OA}$•$\overrightarrow{OB}$+$\overrightarrow{OB}$•$\overrightarrow{OC}$+$\overrightarrow{OC}$•$\overrightarrow{OA}$的值为( )
| A. | 8 | B. | -$4\sqrt{3}$ | C. | 16 | D. | $16\sqrt{3}$ |
16.已知等差数列1,a,b,又4,a+2,b+1为等比数列,求该等差数列的公差( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |
3.(1+ax)(1+$\frac{1}{x}$)5的展开式中常数项为11,则a的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
20.函数y=2+sinx+cosx的最大值是( )
| A. | 2-$\sqrt{2}$ | B. | 2$+\sqrt{2}$ | C. | 2 | D. | 3 |
5.已知全集U={0,1,2,3,4},集合A={0,2,4},B={1,2,3},则A∩(∁UB)为( )
| A. | {0,4} | B. | {2,3,4} | C. | {0,2,4} | D. | {0,2,3,4} |
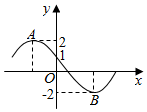 函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.
函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则ω=$\frac{π}{3}$.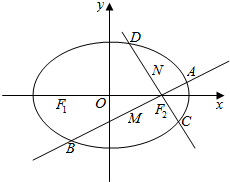 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,且F1,F2与短轴的一个顶点Q构成一个等腰直角三角形,点P($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$)在椭圆C上.